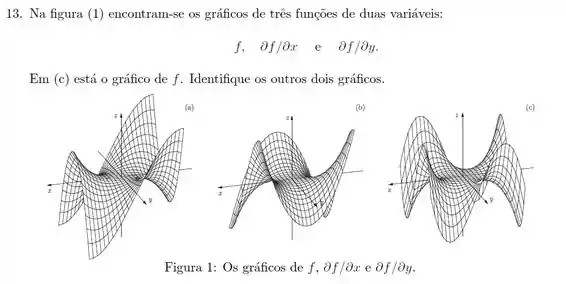
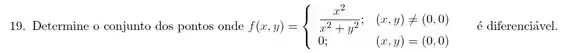Listas GMA de Cálculo IIB da UFF - Lista 3
Cálculo IIB - UFF
Mostre que no ponto a função
Não é contínua, não tem uma das derivadas parciais e não é diferenciável.
Ver solução completaMostre que no ponto a função
Não é contínua, não é diferenciável, porém tem derivadas parciais.
Ver solução completaMostre que no ponto a função
É contínua, tem derivadas parciais, mas não é diferenciável.
Ver solução completaDiga se as afirmativas são verdadeiras ou falsas. Justifique se forem verdadeiras e dê um contraexemplo para as falsas.
Assuma que , , o domínio é aberto e .
- Se é contínua em então é derivável em
- Se é contínua em então possui as derivadas parciais em
- Se possui todas as derivadas parciais em então é contínua em
- Se possui todas as derivadas parciais em então é derivável em
- Se é contínua e possui todas as derivadas parciais em então é derivável em
- Se é derivável em então possui todas as derivadas parciais em
- Se é derivável em então é contínua em
- Se é derivável em então todas as suas derivadas parciais são contínuas em
- Se possui todas as derivadas parciais contínuas em então é derivável em
- Se não possui uma das derivadas parciais em então não é derivável em
- possui todas as derivadas parciais continuas em se, e somente se, é derivável em
Determine a equação de um plano que seja paralelo ao plano
E tangente ao gráfico da função
Ver solução completaSeja .
- Calcule um valor aproximado para a variação em , quando se passa de e para e
- Calcule um valor aproximado para correspondente a e