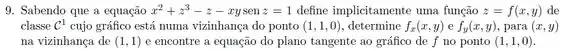
Passo 1
O enunciado já afirma pra gente que a equação
Define implicitamente como uma função de .
Então a gente já pode aplicar direito o teorema da função implícita pra calcular as derivadas que ele pede.
Antes, vamos definir quem é quem.
Temos que é função de , então:
Passo 2
Agora para encontrar a derivada de temos que a fórmula da derivada é
Primeiro, vamos fazer
Passo 3
Agora, vamos calcular
E sua inversa
Passo 4
Agora é só substituir tudo na formula da derivada
Substituindo no ponto :
Passo 5
Agora, a equação do plano tangente é
Onde
Passo 6
As derivadas parciais dessa função nós já calculamos nos passos 3 e 4:
Substituindo em :
Assim
Passo 7
Substituindo tudo na equação do plano tangente: