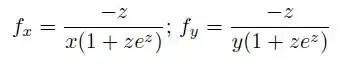Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema da Função Implícita

Ver Teoria
Exercício 22123456789101112131415161718192021232425262728293031323334

Enunciado

Passo 1

Segundo o enunciado, a equação

ln ⁡ ( x y z ) + e z = 1

Define implicitamente z como uma função de x , y .

Assim,

X = ( x , y )

Y = z

Passo 2

Agora para encontrar a derivada de Y = z = g X = g ( x , y ) temos que a fórmula da derivada é

g ' X 0 = - F Y - 1 . F X

Então, primeiro temos que fazer F X

F X = ∂ f 1 ∂ x ∂ f 1 ∂ y = y z x y z x z x y z

F X = ∂ f 1 ∂ x ∂ f 1 ∂ y = 1 x 1 y

Passo 3

Agora, vamos calcular F Y

F Y = ∂ f 1 ∂ z = x y x y z + e z

F Y = ∂ f 1 ∂ z = 1 z + e z

F Y = ∂ f 1 ∂ z = 1 + z e z z

E sua inversa

F Y - 1 = z 1 + z e z

Passo 4

Agora é só substituir tudo na formula da derivada

g ' X 0 = - F Y - 1 . F X

g ' X 0 = ∂ z ∂ x ∂ z ∂ y = - 1 + z e z z - 1 . 1 x 1 y

g ' X 0 = ∂ z ∂ x ∂ z ∂ y = - z 1 + z e z . 1 x 1 y = - z x ( 1 + z e z ) - z y ( 1 + z e z )

Resposta