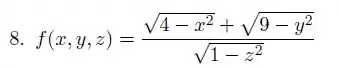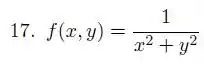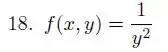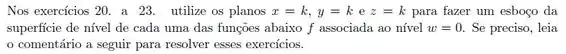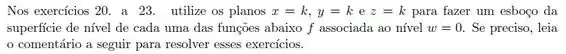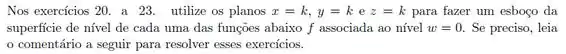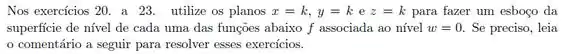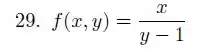Listas GMA de Cálculo IIB da UFF - Lista 1

Descreva e esboce o maior domínio possível da função real de duas variáveis, isto é, descreva analiticamente e represente geometricamente o maior subconjunto do que torna a expressão que define a função verdadeira em .

Descreva e esboce o maior domínio possível da função real de duas variáveis, isto é, descreva analiticamente e represente geometricamente o maior subconjunto do que torna a expressão que define a função verdadeira em .

Descreva e esboce o maior domínio possível da função real de duas variáveis, isto é, descreva analiticamente e represente geometricamente o maior subconjunto do que torna a expressão que define a função verdadeira em .

Descreva e esboce o maior domínio possível da função real de duas variáveis, isto é, descreva analiticamente e represente geometricamente o maior subconjunto do que torna a expressão que define a função verdadeira em .

Considere a função de duas variáveis

Definida em um subconjunto de . Faça um esboço do gráfico de para o caso abaixo

Considere a função de duas variáveis

Definida em um subconjunto de . Faça um esboço do gráfico de para o caso abaixo

Considere a função de duas variáveis

Definida em um subconjunto de . Faça um esboço do gráfico de para o caso abaixo

Considere a função

1. Escreva a equação da curva de nível de que contém o ponto e da curva de nível que contém o ponto
2. Mais geralmente, escreva a equação da curva de nível de que contém o ponto , com .
3. Mostre que o valor de sobre a reta é constante, isto é, que está contida em um conjunto de nível de .
4. Mostre que o valor de sobre a reta é constante, isto é, que está contida em um conjunto de nível de .
5. Se, por um momento, representasse um lucro e você fosse um empresário, em qual reta você gostaria de estar: ou ? Justifique sua resposta.

Esboce as curvas de nível e o gráfico da função

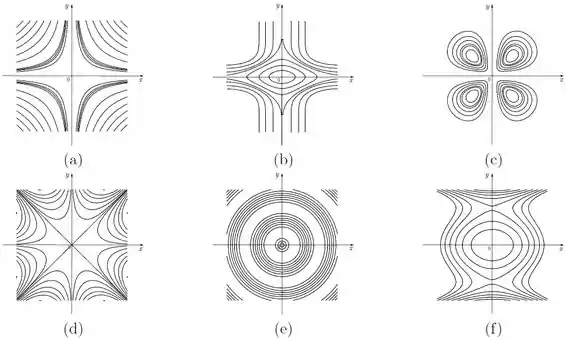
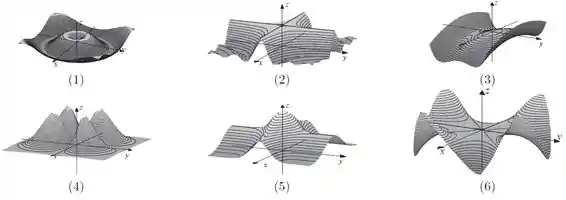
Na figura temos, respectivamente, o desenho das curvas de nível das seis funções a seguir.

Faça a associação destas seis curvas de nível com cada um dos seis gráficos apresentados na figura

As superfícies de nível da função

Associadas aos níveis e podem se cortar? Justifique sua resposta!

Resolva as questões abaixo:

1. Considere a função . Determine os conjuntos de nível de e represente-os geometricamente no sistema de coordenadas adequado (reta, plano ou espaço tridimensional).
2. Considere a função . Determine as curvas de nível de e represente-os geometricamente no sistema de coordenadas adequado (reta, plano ou espaço tridimensional).
3. Considere a função . Determine as superfícies de nível de .
4. Suponha que você chegue em uma sala de aula onde a única sentença escrita no quadro é “Faça um esboço do gráfico da função !”. Que desenho você faria?

Resolva as questões abaixo:

1. Faça o gráfico da função . Escreva uma função cuja curva de nível associado ao nível 0 é igual ao gráfico de .
2. Mais geralmente, dada uma função , escreva uma função cuja curva de nível associada ao nível 0 é igual ao gráfico de . O que você pode dizer a respeito das curvas de nível de para níveis diferentes de 0?
3. Seja z. Escreva uma função cuja superfície de nível associado ao nível 0 é igual ao gráfico de .
4. Mais geralmente, dada uma função , escreva uma função cuja superfície de nível associada ao nível 0 é igual ao gráfico de . O que você pode dizer a respeito das curvas de nível de para níveis diferentes de 0?

De acordo com a lei de gravitação universal de Newton, se uma partícula de massa está na origem de um sistema de coordenadas , então o módulo da força exercida sobre uma partícula de massa situada no ponto é dada por

Onde é a constante de gravitação universal. depende de quantas variáveis? Se e , descreva as superfícies de nível da função resultante.