UFF, Cálculo 2B, Listas, Lista 12, questão 3.
Seja definida por
- Faça um esboço das curvas de nível de associadas aos níveis , e .
- Faça um esboço do gráfico de .
- Mostre que pertence a curva de nível
- Mostre que e
- Mostre que a curva de nível pode ser representada como o gráfico de uma função com .
- Este exercício constitui um contraexemplo para o teorema da função implícita para ? Justifique cuidadosamente sua resposta.
De associada ao nível .
Passo 1
Para esboçar as curvas de nível da função, precisamos fazer
Para
Vamos lá então.
Primeiro para :
Temos a reta
Agora para :
Temos as retas deslocadas
Por fim, para :
Temos as retas deslocadas
Assim, o esboço dessas curvas de nível fica
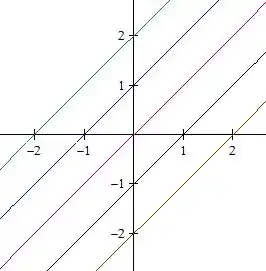
Passo 2
Para esboçar o gráfico de , pense só comigo.
Se fazendo , e obtivemos as retas
Respectivamente, conforme formos aumentando nosso plano , teremos sempre retas cada vez mais deslocadas.
Assim, o gráfico da nossa função fica
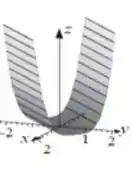
Passo 3
Já vimos na letra que a curva de nível de associada ao nível é a reta
Assim, o ponto pertence a essa curva de nível pois
Ou, podíamos provar isso também verificando que
Passo 4
Vamos calcular e .
Pela regra da cadeia
Substituindo no ponto :
Pronto! Tudo provado!
Passo 5
Conforme já vimos na letra que a curva de nível de associada ao nível é a reta
E essa expressão define como uma função de . Assim
Passo 6
Segundo o teorema da função implícita se e é inversivel, então, numa vizinhança de , a equação
Define implicitamente uma função .
A primeira hipótese nós verificamos na letra , mas a segunda hipótese foi contrariada, conforme vimos na letra . Apesar disso, na letra nós provamos que a função está definida implicitamente na equação
Ué, mas como assim?!
Isso acontece porque a condição , isto é, inversível, é uma condição suficiente, porém não necessária para a existência de uma função implícita .
E é exatamente isso que essa questão nos prova. Assim, ela não é um contraexemplo do teorema da função implícita.
Resposta
