Lista de Exercícios FeMec de Fenômenos Mecânicos da UFABC - Lista 6 - Momento Angular

Uma partícula de massa executa um movimento circular, descrito pelo vetor posição

em que , com e constantes positivas.

(c) calcule , o produto vetorial entre os vetores posição e momento linear.

Uma partícula de massa executa um movimento circular, descrito pelo vetor posição

em que , com e constantes positivas.

(b) mostre que são perpendiculares ao vetor ;

Uma partícula de massa executa um movimento circular, descrito pelo vetor posição

em que , com e constantes positivas.

(a) Determine os vetores velocidade, , e aceleração ;

(b) No caso de uma partícula de massa m, se é seu vetor posição e o seu vetor momento linear, mostre que

Um automóvel que se move a possui pneus com de diâmetro.

Qual é a velocidade angular dos pneus em relação aos respectivos eixos?

Se o carro é freado com aceleração constante e as rodas descrevem voltas completas (sem deslizamento), qual é o módulo da aceleração angular das rodas?

Que distância o carro percorre durante a frenagem?

Um pulsar é uma estrela de nêutrons que gira rapidamente em tomo de si mesma e emite um feixe de rádio, do mesmo modo como um farol emite um feixe luminoso. Recebemos na Terra um pulso de rádio para cada revolução da estrela. O período de rotação de um pulsar é determinado medindo o intervalo de tempo entre os pulsos. O pulsar da nebulosa do Caranguejo tem um período de rotação que está aumentando a uma taxa de .

(a) Qual é a aceleração angular a do pulsar?

(b) Se a se mantiver constante, daqui a quantos anos o pulsar vai parar de girar?

(c) O pulsar foi criado pela explosão de uma supemova observada no ano de 1054. Supondo que a aceleração a se manteve constante, determine o período T logo após a explosão.

Uma partícula de com uma velocidade de está passando pelo ponto . A partícula é puxada por uma força de no sentido negativo do eixo . Quais são, em relação à origem,

o momento angular da partícula

o torque que age sobre a partícula e

a taxa com a qual o momento angular está variando?

Dados dois vetores quaisquer e , dependentes do tempo,

1. Mostre explicitamente que

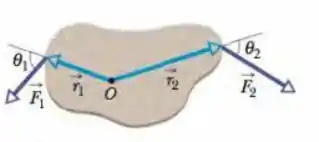
O corpo da figura abaixo, pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se e, qual é o torque resultante em relação ao eixo?

Uma porta de e de largura, suspensa por dobradiças bem azeitadas, está aberta de , ou seja, com seu plano perpendicular ao plano do batente. Ela leva um empurrão na beirada aberta, com um impacto equivalente ao de uma massa de , com velocidade . Quanto tempo ela leva para fechar-se?

Um disco de vinil horizontal de massa e raio gira livremente em torno de um eixo vertical que passa pelo centro com uma velocidade angular de . O momento de inércia do disco em relação ao eixo de rotação é . Um pedaço de massa de vidraceiro úmida de massa cai verticalmente e gruda na borda do disco. Qual é a velocidade angular do disco imediatamente após a massa cair?

Duas partículas se movem em sentidos opostos sobre uma reta. A partícula de massa desloca-se para a direita, com velocidade, enquanto a partícula de massa se desloca para a esquerda, com velocidade. Qual o momento angular total do sistema em relação

(a) ao ponto A,

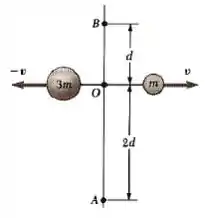(b) ao ponto O e

(c) ao ponto B?

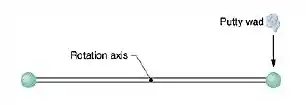
Duas bolas, cada uma de massa M, estão presas às extremidades de uma haste fina de massa desprezível comprimento . A haste está livre para girar sem atrito em um plano vertical em torno de um eixo horizontal que passa pelo centro. Com a haste inicialmente na horizontal, um pedaço de massa de vidraceiro úmida, de massa , cai sobre uma das bolas, batendo nela com uma velocidade de e ficando grudado na bola.

(a) Qual é o módulo da velocidade angular do sistema imediatamente após a batida com a massa de vidraceiro?

(b) Qual o valor mínimo de , em função de e , tal que a haste consiga dar uma volta completa?

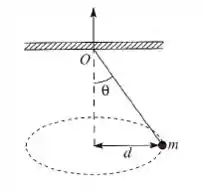
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância do eixo; o ângulo é igual a (ver figura). O fio passa sem atrito através de um orifício numa placa e é puxado lentamente para cima até que o ângulo passa a .

(a) Que comprimento do fio foi puxado?

(b) De que fator variou a velocidade de rotação?

Uma haste metálica delgada, de comprimento e massa , pode girar livremente em torno de um eixo horizontal, que a atravessa perpendicularmente, à distância de uma extremidade. A haste é solta a partir do repouso, na posição horizontal.

(a) Calcule o momento de inércia da haste, com respeito ao eixo em torno da qual ela gira.

(b) Calcule a velocidade angular adquirida pela haste após ter caido de um ângulo , bem como a aceleração .

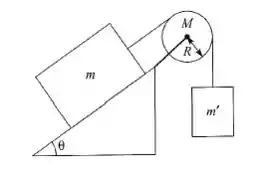
Um bloco de massa , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio e massa , a uma mssa suspensa (vide figura abaixo). O sistema é solto em repouso. Calcule, por conservação de energia, a velocidade de após cair uma altura .

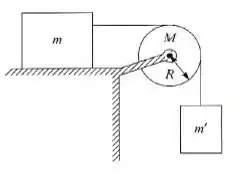
Calcule o efeito da massa da polia, de raio , sobre o sistema da figura abaixo. A masssa , que desliza sem atrito está ligado à massa suspensa pelo fio que passa sobre a polia. Determine (a) a aceleração do sistema; (b) as tensões e nos fios ligados a e .

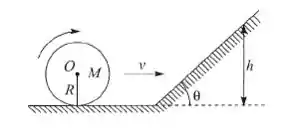
Uma roda cilíndrica homogênea de raio e massa , rola sem deslizar sobre um plano horizontal, deslocando-se com velocidade , e sobe sobre um plano inclinado de inclinação , continuando a rolar sem deslizamento. Até que altura o centro da roda subirá sobre o plano inclinado?

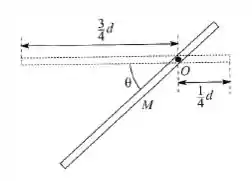
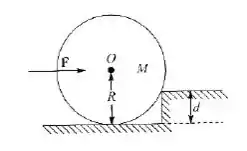
Calcule a magnitude da força horizontal que é preciso aplicar, em direção ao eixo , para conseguir que um tambor cilíndrico, de massa e raio , suba um degrau de altura

Empilham-se blocos idênticos, de comprimento cada um, sobre uma mesa horizontal. Qual é a distância máxima entre as extremidades do ultimo e do primeiro bloco para que a pilha não desabe? Sugestão: Considere as condições de equilíbrio, sucessivamente, de cima para baixo. Faça a experiencia! (use blocos de madeira, livro, tijolos, dominós, ... idênticos).