UFABC – Fenômenos Mecânicos – Lista 6 – Questão 10
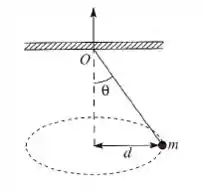
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância do eixo; o ângulo é igual a (ver figura). O fio passa sem atrito através de um orifício numa placa e é puxado lentamente para cima até que o ângulo passa a .
(a) Que comprimento do fio foi puxado?
(b) De que fator variou a velocidade de rotação?
Passo 1
Oi pessoal, tudo bem? Essa questão parece complicada, mas vou facilitar para você!
Temos uma bolinha presa por um fio e esse sistema gira com velocidade angular constante. Em um determinado instante a bolinha é puxada de forma que o ângulo que a corda faz com a vertical passa a ser .
E com essa mudança no comprimento do fio, a velocidade angular também vai mudar! Então a ideia aqui é comparar as situações de força (antes e depois do fio ser puxado) para obter uma relação entre as velocidades angulares e, em conjunto usar a conservação do momento angular dessa bolinha (antes de ser puxada e depois) para determinar quanto o fio foi puxado.
Mas relaxa, vou fazer junto com você! Passo a passo!
Passo 2
Letra (a): Para começar, vamos descrever em termos das forças a dinâmica da bolinha:
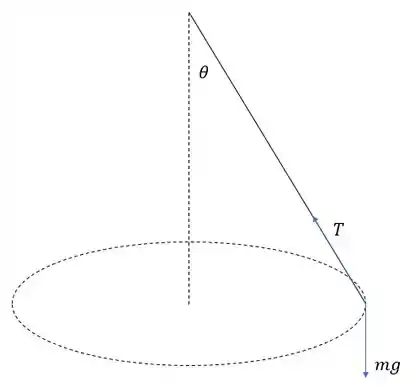
Temos a tensão ao longo do fio, e a força peso verticalmente para baixo.
Lembrando que a força resultante na direção radial (no nosso caso horizontal) é a força centrípeta !
Beleza?
Da situação do desenho, podemos escrever:
Dividindo as duas:
No primeiro instante, o ângulo era
E podemos fazer a mesma análise depois do fio ser puxado!
Depois que a corda é puxada passa a ser
Dividindo as duas:
Assim a relação entre as velocidades angulares e o raio de rotação é
Beleza?
Passo 3
Agora vamos conservar o momento angular!
O momento de inercia de um ponto a gente já conhece! Vale , antes e depois :
Daí temos:
Elevando ao quadrado:
Tranquilo?
Passo 4
Agora podemos juntar resultados! A relação do passo 2:
Com a relação do passo 3:
Substituindo um no outro:
Daqui, como :
Então é essa a distância da bolinha ao eixo de rotação depois do fio ser puxado!
Beleza até aqui?
Passo 5
Ainda precisamos calcular quanto do fio inicial foi puxado!
Bom, para saber quanto foi puxado precisamos primeiro encontrar o comprimento original do fio, quando o ângulo era . Dá uma espiada nessa figura:
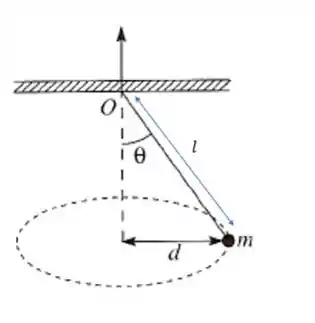
O comprimento do fio pode ser encontrado pelo seno de :
Lembrando que a distância é de , então
Beleza?
Passo 6
Podemos fazer uma análise parecida para verificar o quanto de fio foi puxado. Quando puxamos o fio, digamos por uma distância , formamos o seguinte triângulo:
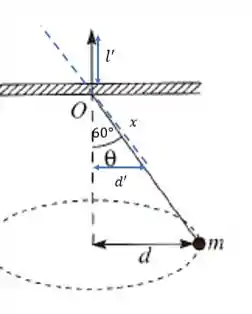
A nova hipotenusa é o , que é o valor do fio que sobrou depois que ele foi puxado. O comprimento que foi puxado é , de forma que .
Vamos primeiro encontrar quanto vale , a partir desse triângulo, já que sabemos quanto vale . E depois é só descobrir quanto vale . Certo?
Vamos lá!
Daí:
Ok? Vamos para letra (b)?
Passo 7
Letra (b): agora queremos a razão entre as velocidades!
Lá do passo 3 encontramos a seguinte relação:
Como calculamos e foi dado, agora é só substituir!
Ufa! Agora sim terminamos!
Espero ter ajudado!