UFABC – Fenômenos Mecânicos – Lista 6 – Questão 18
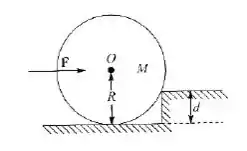
Calcule a magnitude da força horizontal que é preciso aplicar, em direção ao eixo , para conseguir que um tambor cilíndrico, de massa e raio , suba um degrau de altura
Passo 1
Oi pessoal, tudo bem? Essa questão parece bem difícil, mas vou ajudar você aqui!
Vamos lá?
Temos um tambor cilíndrico de raio que está parado e na frente dele tem um degrau, que nem a figura no enunciado mostra:
Queremos descobrir qual é a força (horizontal) necessária para que esse tambor suba o degrau. Para isso acontecer, basta que nossa normal seja nula.
Assim só teremos torque da força peso e da força durante o deslocamento, e eles devem ser iguais:
Agora nossa missão é encontrar os braços de alavanca!
Beleza até aqui?
Passo 2
Mas como vamos achar esses braços?
Pelo desenho!
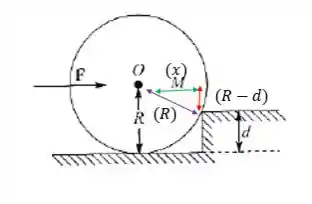
Calculando torque com relação ao ponto de contato (com o degrau):
Lembrando que o braço de alavanca da força peso é a diferença entre o raio do cilindro e a altura do degrau.
E como achamos aquele ?
Pelo teorema de Pitágoras!
Isolando o , temos:
Tranquilo?
Passo 3
Agora é só isolar a força na equação do torque
Substituindo o :
E isolando :
Beleza? Está aí nossa resposta!
Espero ter ajudado!