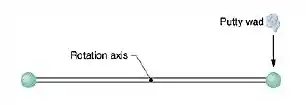
Duas bolas, cada uma de massa M, estão presas às extremidades de uma haste fina de massa desprezível comprimento . A haste está livre para girar sem atrito em um plano vertical em torno de um eixo horizontal que passa pelo centro. Com a haste inicialmente na horizontal, um pedaço de massa de vidraceiro úmida, de massa , cai sobre uma das bolas, batendo nela com uma velocidade de e ficando grudado na bola.
(a) Qual é o módulo da velocidade angular do sistema imediatamente após a batida com a massa de vidraceiro?
(b) Qual o valor mínimo de , em função de e , tal que a haste consiga dar uma volta completa?
Passo 1
Inicialmente, vamos calcular o momento de inércia do sistema bolas-massa:
Substituindos os valores:
E também o momento angular da massa, antes de atingir haste com duas bola:
Substituindo os valores:
Passo 2
Sabendo que na colisão não há torque resultante, então, aplicando a conservação do momento angular, temos:
Isolando e substituindo os valores:
Passo 3
Calculando a relação da energia cinética antes e depois da colisão, temos:
Substituindo os valores:
Passo 4
Para responder esta pergunta, devemos perceber que enquanto a barra gira, a energia mecânica permanece constante. Além disso, perceber que se uma bola sobe uma distância , a outra bola desce a mesma distância , portanto, a energia potencial da haste não muda. Assim, iremos considerar apenas a energia potencial da massa de modelar.

Alpem disso, após a colisão, a massinha descreverá um arco de para baixo até chegar ao ponto mais baixo da trajetória, assim, a energia potencial gravitacional será transformada em energia cinética.
Após atingir o ponto mias baixo, ela descreverá um arco para cima, transformando energia cinética em energia potencial gravitacional, até parar momentaneamente. Então, considerando o ponto mais baixo da trajetória como nível zero de referência para energia potencial, podemos aplicar a lei da conservação da energia mecânica.

Para tanto, vamos considerar que a massa colide com uma das bolas a uma distância do ponto de referência e sua altura no ponto onde para momentaneamente como [fazer analogia com um pêndulo]. Assim, a energia mecânica incial é:
E a energia mecânica final:
Como a haste para momentaneamente, temos:
Então, aplicando a conservação da energia mecânica:
Substituindo os valores:
Isolando :
Isolando :
Como consideramos em função do ponto mais baixo, então o ângulo total de giro é:

Resposta
- ;
- ;
- .