UFABC – Fenômenos Mecânicos – Lista 6 – Questão 06
Duas partículas se movem em sentidos opostos sobre uma reta. A partícula de massa desloca-se para a direita, com velocidade, enquanto a partícula de massa se desloca para a esquerda, com velocidade. Qual o momento angular total do sistema em relação
(a) ao ponto A,
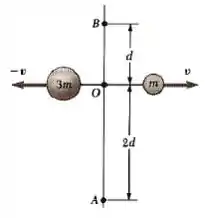(b) ao ponto O e
(c) ao ponto B?
Passo 1
Oi pessoal, tudo bem? Essa questão é de momento angular! Vamos praticar?
O momento angular é o produto vetorial entre o vetor posição e o vetor momento linear de uma partícula. Assim
Beleza?
O vetor pode ser encontrado de acordo com o ponto que se quer calcular o momento angular, e varia de ponto a ponto.
Quando temos mais de uma, o momento angular total é a soma dos momentos angulares das partículas!
Então é isso que o problema pede! Para calcularmos o momento angular total em relação a três pontos diferentes. Então para cada ponto, vamos achar o vetor para cada uma das partículas e jogar naquele determinante
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Letra (a): em relação ao ponto A, temos:
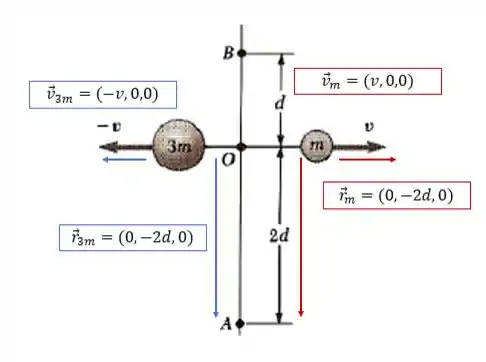
Certo? Nosso próximo passo é calcular o momento angular!
Para a massa :
Beleza?
Agora vamos repetir esse cálculo, mas para a outra massa!
E para a massa :
O momento angular:
E o momento angular total é a soma dos dois:
Tranquilo?
Agora para os outros pontos, é só repetir o mesmo processo: achar os vetores posição e velocidade, jogar no determinante, depois somar os vetores
Passo 3
Letra (b): em relação ao ponto O: ao ponto O, tanto o vetor da massa quando da estão ao longo da mesma direção que as velocidades, logo os vetores são paralelos
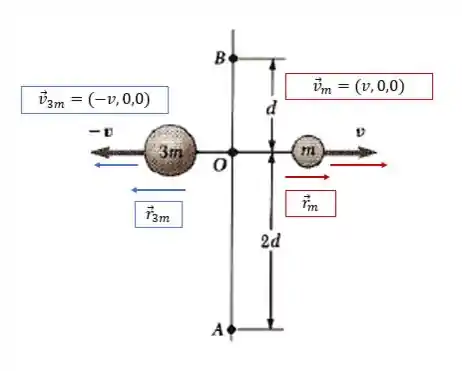
Isso significa que o produto vetorial entre eles é zero
Então o momento angular total é zero!
Beleza? Agora vamos repetir para o ponto B!
Passo 4
Letra (c): em relação ao ponto B temos:
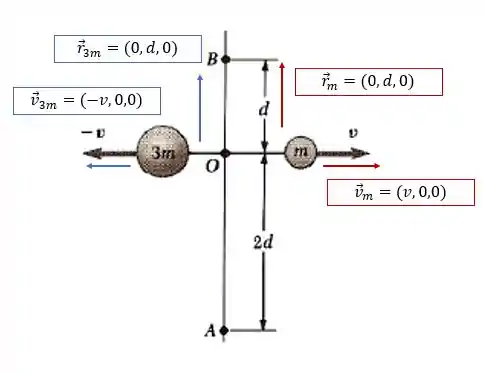
Certo? Nosso próximo passo é calcular o momento angular!
Para a massa :
Certo? Agora para a massa :
O momento angular:
E o momento angular total é a soma dos dois:
Ufa! Terminamos! Espero ter ajudado!