UFABC – Fenômenos Mecânicos – Lista 6 – Questão 14
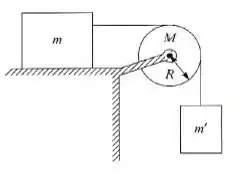
Calcule o efeito da massa da polia, de raio , sobre o sistema da figura abaixo. A masssa , que desliza sem atrito está ligado à massa suspensa pelo fio que passa sobre a polia. Determine (a) a aceleração do sistema; (b) as tensões e nos fios ligados a e .
Passo 1
Oi pessoal, tudo bem? Essa questão parece complicada, mas vou ajudar você aqui! Temos um sistema composto por dois blocos de massas diferentes que estão ligados através de um fio que passa por uma polia. Polia essa que tem massa e raio . O problema pede para calcularmos a aceleração do sistema e as tensões e nos fios ligados a e respectivamente.
Para começar precisamos fazer um diagrama de corpo livre e verificar quais forças estão agindo nesse sistema:
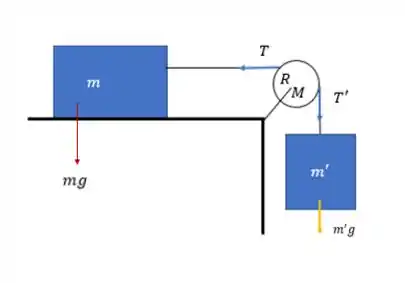
A ideia aqui para encontrar o que é pedido é equacionar as forças, usando a segunda lei de newton para rotações (temos que levar em conta a rotação da polia!) e também a segunda lei de newton para translação (nossa velha conhecida)
mas relaxa, vou fazer passo a passo com você!
Passo 2
Como a massa está pendurada (e portanto o peso faz força no sistema puxando tudo para baixo) e a mesa não tem atrito, podemos considerar que o sistema está acelerado para baixo.
Beleza?
Aplicando a segunda lei de Newton para os blocos (translação pura):
Tranquilo até aqui? Vamos guardar essas equações!
Agora vamos aplicar a segunda lei para rotações na peça dos sitema que está girando: a polia!
Passo 3
Temos duas forças que fazem ela girar: as duas tensões! A tensão faz uma rotação no sentido horário (negativo), equanto que a no sentido anti-horário (positivo).
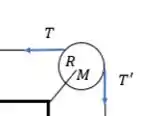
Para a polia, podemos calcular o momento com relação ao seu centro, logo:
Logo,
Essa é a terceira equação que precisamos guardar! E é ela que vamos usar para calcular a aceleração!
(até aqui apenas equacionamos as forças, a questão começa a ser resolvida daqui para frente!)
Passo 4
Letra (a): Mas a gente sabe (da segunda lei para rotações) que , então vamos usar isso!
Como e :
Agora vamos resgatar aquele primeiro conjunto de equações do passo 2:
Isolando as trações no sistema e substituindo em :
Isolando o , temos:
Bora lá!
Passo 5
Letra (b): Por último, podemos calcular as trações. De :
A aceleração é
Daí a tensão :
E para :
Logo,
Beleza? E é isso!
Espero ter ajudado!