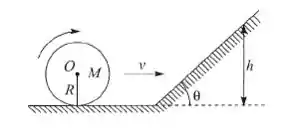
Uma roda cilíndrica homogênea de raio e massa , rola sem deslizar sobre um plano horizontal, deslocando-se com velocidade , e sobe sobre um plano inclinado de inclinação , continuando a rolar sem deslizamento. Até que altura o centro da roda subirá sobre o plano inclinado?
Passo 1
Oi pessoal, tudo bem? Essa questão parece complicada, mas vou te ajudar! Bora lá? Temos um cilindro de raio que está rolando sobre um plano com velocidade . Em certo momento esse cilindro encontra um plano inclinado (com inclinação em relação à horizontal) e começa a subir. Certo ate aqui?


E à medida que sobre no plano inclinado, essa energia cinética vai ser convertida em energia potencial gravitacional (aumentando sua altura, perdendo velocidade)
E a altua máxima é atingida quando toda energia cinética for convertida, ou seja, quando o cilindro tiver velocidade nula.

Então a ideia é essa: usar a conservação de energia para determinar a altura máxima
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Por conservação de energia temos:
Como a roda rola sem deslizar e se move em translação também, inicialmente, o bloco tem energia cinética rotacional e translacional:
Beleza?
E sua energia potencial gravitacional é
Isso porque, mesmo antes de subir o plano, a altura do seu centro de massa é igual ao raio do cilindro, como falamos no passo 1.

Passo 3
Agora, quando o centro de massa atinge a altura máxima a energia cinética do cilindro será nula, já que ele para, então
Certo? Agora vamos juntar tudo isso!

Voltando com esses valores na equação para conservação de energia:
Passo 4
Como :
Como , de acordo com a tabela de momentos de inércia:
Assim, isolando o :
e é isso! Essa é a altura máxima que o cilindro atinge!

Beleza?
Espero ter ajudado!