UFABC – Fenômenos Mecânicos – Lista 6 – Questão 05
O corpo da figura abaixo, pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se e, qual é o torque resultante em relação ao eixo?
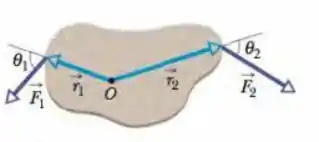
Passo 1
Oi galera, tudo bem? Essa questão é de torque! Vamos praticar?
Torque é o produto da força aplicada pelo baço de alavanca. Neste caso, consideraremos positivo o sentido anti-horário, então produz um torque positivo e produz um torque negativo. A gente pode ver isso desse desenho aqui:
É só fazer uma curva partindo da ponta do vetor força em direção ao vetor deslocamento
Então o torque total fica assim:
Passo 2
Agora que temos a expressão para o torque, basta substituir os valores dados no problema!
Os dados são:
e
Aí temos:
Como , o corpo vai girar no sentido horário.
E é isso! Espero ter ajudado!