UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 7b
Dizemos que dois indutores de auto-indutâncias e e indutância mútua desprezível estão ligados em série quando uma mesma corrente atravessa os dois.
Mostre que esse arranjo pode ser substituído por um único indutor equivalente de auto-indutância e determine em termos de e .
Passo 1
Eaew, belezinha?
Temos aqui um problema de circuitos elétricos em que dois indutores, e , são ligados em série. Como o enunciado indica, nestas condições temos que a corrente ao longo dos indutores é a mesma . Esta alternativa pede para que
Mostre que esse arranjo pode ser substituído por um único indutor equivalente de auto-indutância e determine em termos de e .
Na última alternativa nós fizemos boa parte desse processo! Nós obtivemos a seguinte relação para a tensão no circuito em termos das indutâncias
dentro do seguinte circuito
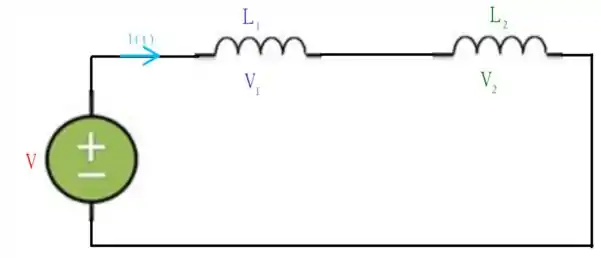
Se você lembrar como definimos uma indutância, será possível identificar diretamente! Saca só!
Passo 2
A indutância é uma constante de proporcionalidade que relaciona a tensão do circuito com a variação temporal de sua corrente através da relação
Se compararmos com o resultado da alternativa anterior, temos que
ou seja, temos que
em geral, não importa quando indutores tenhamos em série, a relação é tal que
A questão foi isso! Te vejo na próxima! Tchau Tchau!