Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.

Determine a intensidade do campo magnético produzido pelo solenóide maior em seu interior, quando ele é atravessado por uma corrente estacionária de intensidade .

Eaew, belezinha?

Esse é um problema longo com várias alternativas, então vamos com calma, tudo bem? O enunciado começa nos apresentando dois solenóides coaxiais de raio e raio . O que isso quer dizer? Quer dizer que temos um solenóide dentro do outro, de forma que o campo magnético gerado por eles ao passarmos uma corrente elétrica estarão na mesma direção . Um solenóide é um objeto físico que pode ser representado da seguinte maneira

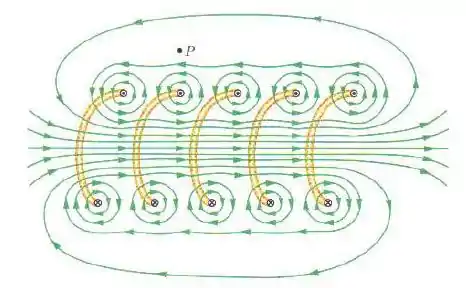
Os fios em amarelo são percorridos pela corrente, e as linhas de campo magnético em verde dependem do sentido em que essa corrente percorre (em nosso caso temos um desses solenóides dentro do outro). A intensidade do campo magnético depende intimamente da densidade de espiras por unidade comprimento, em nosso caso e , para o solenóide menor e maior respectivamente! A primeira alternativa nos pede

Determine a intensidade do campo magnético produzido pelo solenóide maior em seu interior, quando ele é atravessado por uma corrente estacionária de intensidade .

Ou seja, vamos esquecer o solenóide menor por agora e focar no maior! A intensidade do campo magnético é obtida diretamente da intensidade de corrente dada , e das características do solenóide. Você lembra qual é a formulinha? Saca só!