UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 2c
Um cabo coaxial é formado por um cilindro circular reto, condutor, maciço, de raio e uma casca cilíndrica condutora de raio , coaxial ao cilindro. Uma corrente estacionária de intensidade flui ao longo do eixo do cilindro, uniformemente distribuída sobre sua seção transversal, e uma corrente estacionária de mesma intensidade flui ao longo da casca cilíndrica, em sentido oposto à do cilindro.
A partir do resultado acima, determine a auto-indutância por unidade de comprimento deste cabo.
Passo 1
Oiie tudo bem?
O sistema que o enunciado descreve um sistema que pode ser visto da seguinte forma
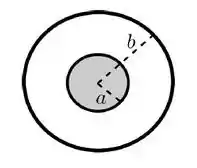
imagine que o círculo de raio é o corte transversal da casca cilíndrica e tem uma corrente que aponta para dentro da tela, e que o disco no interior é o corte transversal do cilindro maciço em seu interior com uma corrente que sai da tela! A intensidade desta corrente é tanto na superfície cilíndrica quanto no cilindro maciço, e temos a informação adicional que a corrente é uniformemente distribuída transversalmente pelo cilindro, ou seja
em que é a densidade de corrente e é uma área transversal! Esta alternativa nos pede
A partir do resultado acima, determine a auto-indutância por unidade de comprimento deste cabo.
O resultado acima citado é o fluxo magnético calculado na alternativa anterior, temos que
Isso nos dá a resposta quase que diretamente! Precisamos lembrar que a auto-indutância é constante de proporcionalidade da força-eletromotriz com a variação da corrente que passa pelo cabo! Ou seja
Vamos usar essa informação e a lei de Faraday-Lenz para identificar quem é ! Saca só!
Passo 2
Se derivarmos o fluxo em relação ao tempo, e considerarmos que , temos que
Usando que
obtemos
Note que podemos comparar a expressão do passo com a obtida aqui e dizer que
A questão foi isso! Te vejo na próxima! Tchau Tchau!