UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 2a
Um cabo coaxial é formado por um cilindro circular reto, condutor, maciço, de raio e uma casca cilíndrica condutora de raio , coaxial ao cilindro. Uma corrente estacionária de intensidade flui ao longo do eixo do cilindro, uniformemente distribuída sobre sua seção transversal, e uma corrente estacionária de mesma intensidade flui ao longo da casca cilíndrica, em sentido oposto à do cilindro.
Utilizando a lei de Ampère, determine a intensidade do campo magnético no interior da região entre o cilindro e a casca, ou seja, para , onde é a distância ao eixo do cilindro.
Passo 1
Oiie tudo bem?
O sistema que o enunciado descreve um sistema que pode ser visto da seguinte forma
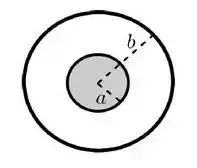
imagine que o círculo de raio é o corte transversal da casca cilíndrica e tem uma corrente que aponta para dentro da tela, e que o disco no interior é o corte transversal do cilindro maciço em seu interior com uma corrente que sai da tela! A intensidade desta corrente é tanto na superfície cilíndrica quanto no cilindro maciço, e temos a informação adicional que a corrente é uniformemente distribuída transversalmente pelo cilindro, ou seja
em que é a densidade de corrente e é uma área transversal! A primeira alternativa nos pede
Utilizando a lei de Ampère, determine a intensidade do campo magnético no interior da região entre o cilindro e a casca, ou seja, para , onde é a distância ao eixo do cilindro.
Mas quem é a lei de Ampère? Ela tem o seguinte formato
em que é a permeabilidade magnética do vácuo, é o campo magnético desejado, é a corrente interna a curva , em que a mesma é uma curva fechada chamada amperiana! Vamos usar essas informações para resolver nosso problema!
Passo 2
Essa primeira alternativa é a mais direta! Note que como estamos querendo o campo magnético em um ponto que dista do eixo do cilindro, em que , podemos escolher uma amperiana que é uma curva circular de raio , sendo assim, temos que é um vetor tangente a curva em todo o seu comprimento, sendo assim, como as linhas de campo são circunferências ao redor do cilindro maciço (regra do parafuso), podemos simplificar a lei de Ampère para obter
e, tendo em vista que a curva é externa ao cilindro maciço, temos que
e, desta forma
A integral do lado esquerdo é a circunferência da amperiana, como ela é um círculo de raio , obtemos que
e, a intensidade do campo é
A primeira alternativa foi isso! Te vejo na próxima! Até já!