UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 8b
Dizemos que dois indutores de auto-indutância e e indutância mútua desprezível estão ligados em paralelo quando eles estão submetidos à mesma diferença de potencial elétrico .
Mostre que esse arranjo pode ser substituído por um único indutor equivalente de auto-indutância e determine em termos de e .
Passo 1
Oiiie, tudo certinho?
Novamente temos dois indutores de indutância, e , mas agora ligados em paralelo como seguinte circuito
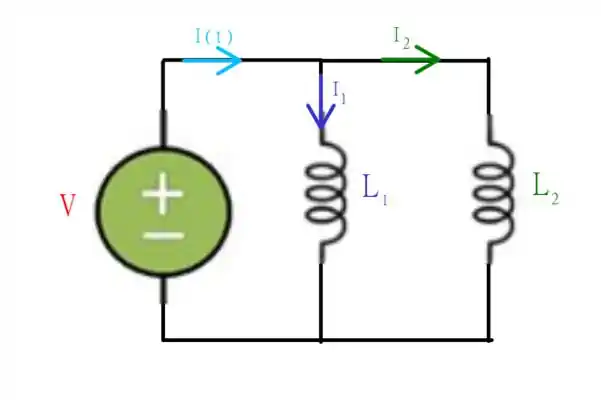
Note que neste circuito os dois indutores estão sobre a mesma diferença de potencial , mas a corrente individual entre eles é diferente! A alternativa nos pede para que
Mostre que esse arranjo pode ser substituído por um único indutor equivalente de auto-indutância e determine em termos de e .
Aqui precisamos usar o resultado da alternativa anterior
e a definição de indutância! E, assim, iremos identificar diretamente quem é a nossa indutância equivalente! Saca só!
Passo 2
Da definição de indutância temos que
Como a variação da corrente no passo e essa variação são a mesma, temos que
de forma que podemos identificar que
a questão foi isso! te vejo na próxima! Tchau Tchau!