Um cabo coaxial é formado por um cilindro circular reto, condutor, maciço, de raio e uma casca cilíndrica condutora de raio , coaxial ao cilindro. Uma corrente estacionária de intensidade flui ao longo do eixo do cilindro, uniformemente distribuída sobre sua seção transversal, e uma corrente estacionária de mesma intensidade flui ao longo da casca cilíndrica, em sentido oposto à do cilindro.

Calcule o fluxo de campo magnético através de uma superfície retangular com dois lados paralelos à direção radial, se estendendo por toda a região do item anterior, e dois lados paralelos ao eixo do cabo, de comprimento .

Oiie tudo bem?

O sistema que o enunciado descreve um sistema que pode ser visto da seguinte forma

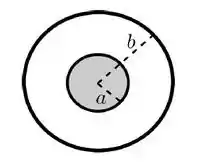
imagine que o círculo de raio é o corte transversal da casca cilíndrica e tem uma corrente que aponta para dentro da tela, e que o disco no interior é o corte transversal do cilindro maciço em seu interior com uma corrente que sai da tela! A intensidade desta corrente é tanto na superfície cilíndrica quanto no cilindro maciço, e temos a informação adicional que a corrente é uniformemente distribuída transversalmente pelo cilindro, ou seja

em que é a densidade de corrente e é uma área transversal! Esta alternativa nos pede

Calcule o fluxo de campo magnético através de uma superfície retangular com dois lados paralelos à direção radial, se estendendo por toda a região do item anterior, e dois lados paralelos ao eixo do cabo, de comprimento .

Na alternativa anterior obtivemos com a seguinte intensidade

esse campo tem direção e sentido dada pela regra da mão direita e a expressão acima é válida para qualquer que obedeça

A direção deste cilindro é tal que ele cruza a superfície retangular descrita perpendicularmente! O que é bastante útil para nós, uma vez que queremos o fluxo deste campo ao longo desta superfície retangular, dada por

em que é o elemento de área da superfície! Vamos usar isso tudo para calcular o fluxo!