UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 4a
Considere um solenóide toroidal de raio médio , com seção transversal de área e voltas de fio enroladas de forma compacta ao longo de seu comprimento.
Utilizando a lei de Ampère, determine a intensidade do campo magnético a uma distância da origem (eixo do toróide). Assuma que as linhas de campo no interior do solenóide são circulares (e de fato são, mesmo nessa situação arbitrária).
Passo 1
Eaew, tudo certinho com você?
O esquema que o enunciado descreve tem o seguinte formato
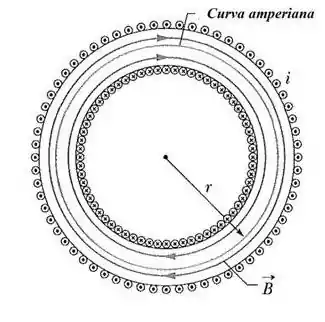
em que é o raio médio. A área transversal deste toróide é e temos que o fio dá voltas compactadas ao longo do toróide. A alternativa nos pede para que
Utilizando a lei de Ampère, determine a intensidade do campo magnético a uma distância da origem (eixo do toróide). Assuma que as linhas de campo no interior do solenóide são circulares (e de fato são, mesmo nessa situação arbitrária).
Ou seja, precisamos usar a lei de Ampère dada por
em que é o campo magnético desejado (as linhas de campo circulares indicadas na figura), é um vetor infinitesimal sempre tangente a curva , uma amperiana escolhida de maneira conveniente para calcularmos o campo magnéticos a uma distância arbitrária do centro do toróide. Ou seja, resolver este problema é encontrar uma relação válida entre as grandezas acima! Vamos tentar fazer isso!
Passo 2
Primeiro, como indicada na figura, vamos escolher uma amperiana que é uma circunferência de raio como indicada na figura, sendo assim, podemos garantir que a simetria indicada no enunciado para o campo magnético nos leva à
e, a integral se torna
Note que a integral do lado esquerdo é simplesmente a circunferência da curva amperiana, portanto, temos que
e, o campo magnético será da forma
Agora, quem é essa corrente interna?
Passo 3
A corrente interna é toda corrente que está interior a amperiana escolhida! Devido a geometria do toróide temos que a corrente cruza o interior da amperiana vezes (devido as voltas realizadas), sendo assim, temos que o campo magnético é dado por
Essa alternativa foi isso! Te vejo na próxima! Até já!