UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 5
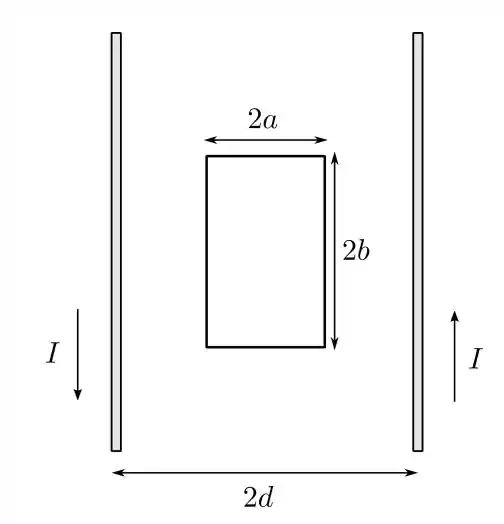
Uma espira condutora retangular de lados e é posicionada no mesmo plano que um par de fios condutores finos, retilíneos e paralelos, como mostrado na figura abaixo. Os fios transportam correntes estacionárias de mesma intensidade e sentidos opostos e estão separadas por uma distância , como indicado. O centro da espira está equidistante dos fios e os lados de comprimento são paralelos a eles. Determine a indutância mútua entre a espira e o par de fios.
Passo 1
Oiie, tudo certinho?
O esquema descrito no enunciado é resumido através da figura
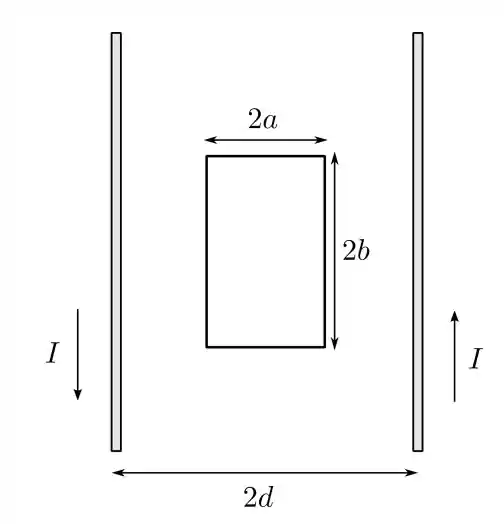
note que a espira central está centralizada e a corrente nos fios paralelos têm direções opostas! Estas condições são importantes para o que precisamos fazer! Nós devemos calcular a indutância mútua entre as os fios e a espira central, essa indutância mútua é definida tal que
A vantagem que temos aqui é o fato de que não importa se calculamos o efeito dos fios sobre a espira, ou da espira sobre os fios, a indutância mútua é a mesma! Então vamos fazer o mais fácil e obter a influência dos fios sobre a espira! Saca só!
Passo 2
Vamos calcular a indutância através da relação
Para calcularmos o fluxo indicado note que a direção das correntes no fio é bastante importante, na distribuição indicada, usando a regra do parafuso com sua mão direita, você verá que ambos os fios geram campos magnéticos que se somam no centro, ou seja, a corrente total que gera o campo que atua na espira é dada por
e, o campo magnético é a superposição do campo magnético de dois fios, ou seja
em que , é a distância do centro da espira! Ou seja, o campo atuando é
Vamos calcular o fluxo agora!
Passo 3
Como o campo magnético cruza a área transversal da espira central perpendicularmente, podemos garantir que o fluxo é simplificado para
usando que a espira é retangular, temos que
e, portanto, usando o campo magnético obtido, temos um fluxo dado por
Finalmente, a indutância mútua é dada por
como temos apenas uma espira , e simplificando a expressão acima, obtemos
A questão foi isso! Te vejo na próxima! Tchau Tchau!