15) Um comprimido é produzido em série numa empresa farmacêutica com peso médio de e desvio padrão de com distribuição normal. Os comprimidos passam por um controle de qualidade e os comprimidos com peso menor que e peso maior que são eliminados do lote. Qual a probabilidade de nesse lote restante retirarmos ao acaso um comprimido com peso entre os valores e ?

a)

b)

c)

d)

e)

Vamos começar calculando a probabilidade .

Se pensarmos nessa probabilidade pela função de densidade, estamos querendo calcular a área abaixo da curva entre e .

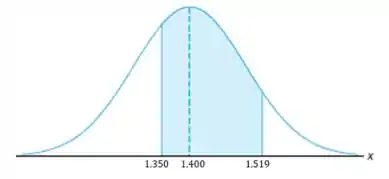
É como uma subtração entre toda a área antes de e toda a área antes de . Mas, como isso é a curva de densidade de probabilidade, essas áreas valem justamente e , respectivamente.

Massa! Concluímos que:

Show! Normalizando esses valores temos:

Logo, pela Tabela normal (muito importante essa tabela hein galera), temos:

Analogamente, para , temos:

Usando a tabela normal, vem:

Excelente! Então finalizando essa primeira parte, temos:

Prontinho 😊

Vamos calcular agora . Usando o mesmo raciocínio do passo anterior, podemos escrever que:

Também do passo anterior, já sabemos que:

Além disso, lembra que é justamente a média da distribuição normal. E, a probabilidade de termos é sempre .

Daí, rapidamente temos que:

Muito bom pessoal! Tudo legal até aqui?

Já estamos com a faca e o queijo na mão, é só dar o golpe final! Lembra que:

Daí, substituído os valores que encontramos, temos:

Portantooo...

Top galera! Essa foi a nossa questão, espero que vocês tenham entendido bem direitinho.

Até a próxima 😊