Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Probabilidade Conjunta de V.A. Bidimensionais Contínuas

Ver Teoria
Exercício 2612345678910111213141516171819202122232425272829303132

Enunciado

USP probabilidade P3 2018

Obtenha P X > Y , se a função de densidade de probabilidade conjunta das variáveis aleatórias X ,   e   Y é:

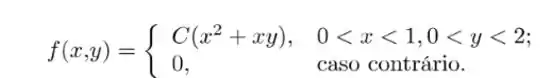
Passo 1

Boa, galera. Queremos calcular P X > Y , mas antes disso precisamos descobrir quem é a constante normalizadora C   . Vale lembrar que essa constante é responsável por fazer a integral no domínio da f     ser igual a 1   .

Integrando f   temos:

∫ 0 2 ∫ 0 1 C x 2   + x y d x d y   =   1

⇒   ∫ 0 2 ∫ 0 1 C x 2   + x y d x d y   =   =   C ∫ 0 2 x 3 3   +   x 2 y 2 ​ x = 0 x = 1 d y

=   C ∫ 0 2 1 3   +   1 y 2   d y

=   C y 3   +   y 2 4   ​ y = 0 y = 2  

=   C 2 3   +   1    

Logo C 2 3   +   1     = 1

⇒   C   = 3 5

Passo 2

Agora que temos a constante normalizadora C   , podemos calcular P X > Y .

P X > Y = ∫ 0 1 ∫ y 1 3 5 x 2   + x y d x d y   (note que estamos fazendo y até 1, pois para valores maiores a probabilidade de x será zero, i.e P X > y   =   0   se   y > 1 )

(para melhor entender o porquê dessa integral vamos pensar no caso discreto. No caso discreto poderíamos separar a P X > Y como a soma de todas as probabilidades onde x > y   acontece. É exatamente isso que estamos fzendo no caso contínuo. Estamos integrando/“somando” todos os casos onde x > y   para todos os valores possíveis de y   )

∫ 0 1 ∫ y 1 3 5 x 2   + x y d x d y   =   3 5 ∫ 0 1 x 3 3   +   x 2 y 2 ​ x = y x = 1 d y

=   3 5 ∫ 0 1 1 3   +   y 2   -   y 3 3   -   y 3 2 d y

= 3 5 ∫ 0 1 1 3   +   y 2   -   5 y 3 6 d y

= 3 5 y 3   +   y 2 4   -   5 y 4 24 ​ y = 0 y = 1

= 3 5 1 3   +   1 4   -   5 24  

=   3 5 ⋅ 3 8 =   9 40

Resposta

  9 40

Exercícios de Livros Relacionados

Suponha que duas variáveis aleatórias (X,Y) sejam uniformemente distribuídas num círculo de raio a. Então, a função de densidade de probabilidade conjunta é: f x , y = 1 π a 2 ,x 2 + y 2 ≤ a 2 f ( x ,
A distribuição de probabilidade conjunta é. Mostre que a correlação entre X e Y é zero, porém X e Y não são independentes.
Os pesos de tijolos de barro usadas em construção são distribuídas normalmente, com uma média de três libras e o desvio padrão de 0.25 libras. Suponha que os pesos dos tijolos sejam independentes e qu
Suponha que as variáveis aleatórias, existem uma função densidade de probabilidade conjunta. Determine o seguinte:
Suponha que é correlação entre X e Y seja P. Para as constantes a, b, c e d qual é a correlação entre as variáveis aleatórias