USP probabilidade P3 2018
A função de densidade de probabilidade conjunta para duas variáveis aleatórias para uma constante é dada por:
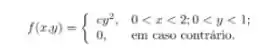
A densidade marginal de para
Passo 1
Fala pessoal. Tudo beleza? Vamos para mais uma questão de probabilidade.
Para essa questão precisamos calcular a densidade marginal de . A marginal de é dada por:
Ou seja, fazemos a “soma” da distribuição conjunta em todos os valores de .
Vamos calcular essa densidade marginal.
Passo 2
Agora que temos a distribuição marginal de em função da constante , precisamos calcular essa constante. Como a marginal de é uma função de densidade sua integral em todo o domínio tem que ser ou seja,
Passo 3
Agora que temos o valor da constante obtemos a marginal de
Resposta
Exercícios de Livros Relacionados
Suponha que duas variáveis aleatórias (X,Y) sejam uniformemente distribuídas num círculo de raio a. Então, a função de densidade de probabilidade conjunta é: f x , y = 1 π a 2 ,x 2 + y 2 ≤ a 2 f ( x ,
A distribuição de probabilidade conjunta é. Mostre que a correlação entre X e Y é zero, porém X e Y não são independentes.
Os pesos de tijolos de barro usadas em construção são distribuídas normalmente, com uma média de três libras e o desvio padrão de 0.25 libras. Suponha que os pesos dos tijolos sejam independentes e qu
Suponha que as variáveis aleatórias, existem uma função densidade de probabilidade conjunta. Determine o seguinte:
Suponha que é correlação entre X e Y seja P. Para as constantes a, b, c e d qual é a correlação entre as variáveis aleatórias