13) Dimensione o comprimento médio de uma prateleira para acomodar latas quadradas de tinta que tem larguras normais de valor esperado e desvio padrão . Deseja-se que as latas escolhidas aleatoriamente (de forma independente) caibam na prateleira e que a probabilidade de deixarem uma folga menor que entre a última lata e o final da prateleira seja menor que . Admita que as latas foram encostadas à esquerda no início da prateleira.
a)
b) 0
c)
d)
e)
Passo 1
Faaaala galerinha do Responde Aí, como é que vocês estão? Tudo certinho?
Essa questão é muuuuito interessante, e um tanto quanto difícil haha. Mas vamo junto comigo que vai ficar facinho facinho 😉
Basicamente, temos latas quadradas de tinta que seguem uma distribuição normal, com média de e desvio padrão de .
Daí, resolve-se criar uma prateleira pra acomodar dessas latas, que serão escolhidas aleatoriamente, de modo que a probabilidade de haver uma folga menor que seja menor que . Bora esquematizar essa situação pra facilitar um pouco o entendimento.
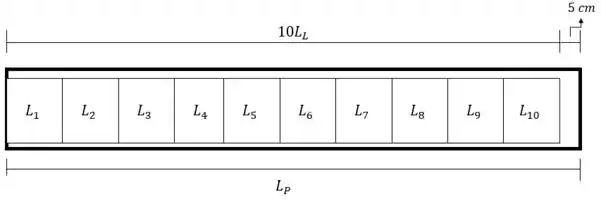
Essa é uma visão superior da prateleira. representa cada uma das latas colocadas, o comprimento total delas é dado por . Já é a variável aleatória que representa o tamanho da prateleira.
Consideramos uma folga de , nesse caso podemos considerar que:
Eaí, conseguiram entender o que tá acontecendo?

Show! Vamo simbora!
Passo 2
Bom, precisamos calcular o comprimento médio de . Mas, qual que é a distribuição dessa variável aleatória?

Como está relacionado com o tamanho das latas, usando o teorema central do limite, podemos afirmar que também segue uma distribuição normal.
Assim, podemos chamar:
Consequentemente, também será uma variável aleatória com distribuição normal, pois é a combinação de duas V.A’s normais. Sacaram?
Daí, temos que:
Como seguem uma distribuição normal, podemos buscar a distribuição padrão, normalizando. Daí:
Massa! Então, precisamos determinar e né?!
Pelas propriedades da esperança, sabemos que:
Logo, para vamos ter:
Mas, como é dito que que a largura média das latas é de , vem:
Top! Também sabemos que:
E que:
Daí, vem:
No enunciado é falado que . Como , vem:
Po, até agora tudo beleza, mas e pra determinar , o que podemos fazer?

Hahaha. Essa sacada é bem interessante. Pensa comigo, pra gente ter um desvio padrão precisamos ter vários elementos em uma amostra, mas nessa situação temos apenas uma prateleira. Ou seja, temos:
Excelente! Substituindo lá em cima, temos:
Daí:
Prontinho!!
Passo 3
c) Agora já podemos calcular :
Para esse valor de devemos ter que:
Daí, consultando a tabela normal, na igualdade vamos ter que:
Logo:
Isolando , temos:
É isso galera, gostaram?
Essa questão é bem complicadinha, tem umas passagens um pouco complicadas, mas espero que tenha ficado bem claro pra vocês! Até a próxima 😉
Resposta
Letra E: .