Calcule os limites.
Passo 1
Galera, pra calcular o limite de uma função vetorial, podemos tomar individualmente o limite de cada uma das funções componentes. Então,
Os dois primeiros deram certo, mas no terceiro caímos em uma indeterminação, então precisaremos fazer esse limite de maneira diferente.
Passo 2
Como o terceiro limite tem uma indeterminação, vamos usar a greda de L’Hôpital. Ela nos ajuda a achar o limite de uma fração quando o limite do numerador e do denominador nos levam a uma indeterminação.
Mas você pode estar pensando: “mas ali não temos uma fração”. E é por isso que antes de tudo, vamos transformá-la em fração:
Fazemos isso lebrando que quando temos uma fração embaixo no denominador, nós jagamos ela pra cima invertida multiplicando o numerado. Assim ó:
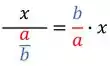
No nosso caso, temos o . Vamos escrever esse como e fazer o processo inverso, jogando ele pra baixo invertido:
Agora que já está na forma de fração, vamos aplicar a regra do L’Hôpital
Nela faremos a derivada do numerador e do denominador e aplicaremos o limite no resultado que encontrarmos.
Derivando o numerador temos:
E derivando o denominador:
Assim, nosso limite se transforma em:
Ainda tá bem feio isso aí. Pra melhora a forma como está escrito, lembramos que na divisão de frações, nós repetimos a de cima e multiplicamos pela inverso da de baixo:
Simplificando um de cima com o de baixo, nossa função ficará:
Bem melhor, né?
Agora, finalmente a gente aplica o limite
Ufa e depois de tudo isso, concluímos: