Determine o domínio das funções vetoriais.
Passo 1
Como vocês estão, galera?
Esse é mais um exercício de determinar o domínio de uma função vetorial .
Como uma função vetorial tem várias funções dentro dela, podemos nomear cada uma dessas funções para a gente se organizar.
A função do primeiro componente pode se chamar .
A função do segundo componente pode se chamar .
Por fim, a função do terceiro componente pode se chamar .
Temos então:

Beleza, fizemos isso para deixar nossa solução mais organizada. Mas ainda resta responder uma pergunta: o que exatamente significa determinar o domínio?

Determinar o domínio é achar os valores de que não causam problema de conta nas funções , e .
Para ficar mais claro o que são esses problemas de conta, vamos ver o próximo passo!
Passo 2
Para a gente achar os valores de que não fazem as funções , e terem um problema de conta, a gente precisa descobrir os valores de que causam problemas de conta.
Existem três situações muito comuns de acontecerem:
- Divisão por zero. Sempre que a função tiver uma fração, temos que garantir que o denominador não vale zero!
- Raiz quadrada de número negativo. Sempre que a função tiver uma raiz quadrada, temos que garantir que a parte de dentro da raiz nunca seja negativa.
- de número menor ou igual a zero. Sempre que uma função tiver um , precisamos garantir que a parte de dentro do seja maior que zero!
Para achar todos os problemas de conta, temos que procurar em cada uma das três funções uma raiz quadrada, uma fração e um .
De cara nós podemos ver que a função tem uma raiz quadrada.
Logo, nós temos que garantir que a parte de dentro dessa raiz não seja negativa. Ou seja, essa parte de dentro precisa ser maior ou igual a zero.
Passando o para o lado direito, fazemos o sinal de menos sumir.
Vamos só trocar de lado pra ficar mais fácil de ler. Ahh, não esquece de trocar o sinal também, ok!
A expressão acima diz que tem que ser menor ou igual a . Para ser menor ou igual a , tem que estar entre o e o .
Vamos ver isso em uma reta numérica que vai ficar mais claro:
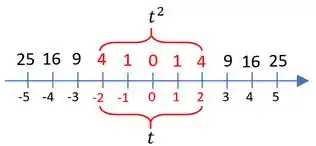
Perceba que valores menores que nos darão maior que , e valores, maiores que , também.
Assim:
Ou seja, tem que valer entre e para não causar um problema de conta na função .
No próximo passo, vamos verificar os valores de que podem causar erro de conta nas funções e .
Passo 3
Vamos olhar para a função e procurar uma raiz quadrada, uma fração ou um nela.
Ela não tem nada disso, certo? Logo, nenhum valor de pode causar um erro de conta em . Então dizemos que seu domínio são todos os números Reais .
Por fim, vamos olhar para .
Ele tem um . Então, a parte de dentro dele tem que ser maior que zero! Logo:
Agora, vamos passar o para o lado direito.
Isso quer dizer que o tem que ser maior que para não causar nenhum problema de conta em .
Passo 4
Então a gente tem duas condições, a primeira definida em e a terceira definida em
Vamos ver visualmente como juntar essas duas condições!
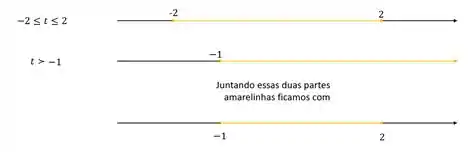
Nossos valores de precisam estar entre e , incluindo esses valores, mas também precisamo ser maiores que . Quando acontece isso a gente pega os valores que respeitam as duas condições ao mesmo tempo.
Então nosso intervalo é:
Se ficar dentro desse intervalo, ele não vai dar problema de conta em nenhuma das três funções que existem dentro da função vetorial .
Logo o domínio de são justamente esses valores de !
Pronto! Determinamos o domínio!
Resposta
Dominio de :