Determine e esboce o domínio da função
Passo 1
Fala, pessoal, prontos para iniciar nossos estudos sobre funções vetoriais?
Primeiro de tudo, nós podemos perceber que essa é uma função bem diferente! Ela é é uma função em ! Ela tem duas funções separadas por uma vírgula! A primeira (da esquerda) é uma função de e a segunda (a da direita) é uma função de .
Como essa é uma função que tem duas funções dentro dela, vamos dar um nome para cada função diferente. Vamos chamar a função de da esquerda de e a função de da direita de função .
Nós separamos a função vetorial em duas funções, mas precisamos entender o que o enunciado quer. Ele pediu para a gente determinar o domínio da função vetorial . Então vamos do começo,Mas o que é o domínio?

O domínio são todos os valores de e de que não causam problemas de conta nas funções e que fazem parte da nossae .
Por exemplo, vamos ver o que acontece quando vale na função ?!
Através da equação acima, Vvemos que, quando vale , o valor da função não pode ser calculado. Isso acontece, porque gera uma divisão por zero que é impossível de ser calculada! Em outras palavras, o valorOu seja, dá problema de conta na função ! Por isso, dizemos que não pode fazer parte do domínio de ! tem que ser diferente de zero!
Com esse exemploAssim, conseguimos ver que, para saber quais os valores que e podem ter, e determinar o domínio, precisamos antes saber quais os valores eles que e não pode ter!
Então vamos procurar no próximo passo quais os outros valores que não pode ter.
Passo 2
Nesse passo, nós vamos procurar os outros valores que não pode ter. Para isso,P precisamos descobrir os valores de que dão problema de conta em .!
As funções que estão dentro da função vetorial sempre dão dicas de como achar esses valores!
Por exemplo, sempre que uma raiz quadrada aparece, temos que ficar atentos!
Devemos ter atenção nela, porque raiz quadrada de número negativo não existe! A raiz quadrada de número negativo não pode ser calculada no conjuto dos número reais e, portanto é um problema de conta!
Como o está dentro da raiz quadrada, ele não pode ser negativo. Isso significa que ele precisa ser maior ou igual a zero.
No entanto, já vimos que sabemos que não pode sernão pode valer zero, porque o zero também causa um erro de conta. Ou seja, tem que ser maior que zero, pois só assim ele não será igual a zero e nem negativo..
Logo, todos os valores de maiores que zero fazem parte do domínio!
Agora, vamos descobrir quais os valores que o não pode ter.
Passo 3
Para descobrir quais os valores que não pode ter, precisamos prestar atenção na raiz quadrada de .
A parte de dentro dessa raiz quadrada (que nesse caso é o ) não pode ser negativa, porque isso levaria a um erro de conta! Ou seja, tem que ser maior ou igual a zero.
Aqui você pode pensar, “mas ele já é negativo, porque tem esse menos ali na frente”. Mas na verdade o valor que ficará dentro da raiz vai depender do sinal do número que colocarmos no lugar do . Vamos ver um exemplo pra entender melhor isso.
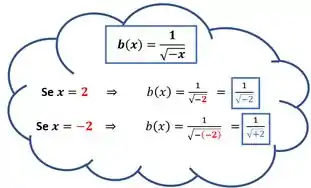
Veja que se o for positivo, nossa raiz ficará negativa, o que não pode acontecer (como aconteceu quando ). Já se o for negativo, o sinal de menos na frente dele fará com que ele se torne positivo e assim não teremos nunhum erro de conta (como quando .
Então, o que precisamos é que a raiz não seja nengativa, e para isso:Se a gente passar o para o outro lado, vemos que:
Mas há outro detalhe ali. Nossa raiz está no denominador, e vimos que se ela for zero, teremos uma divisão por zero. O que também não pode acontecer.
Então
E para isso precisamos que Isso significa que, para o ser maior ou igual a zero, precisa ser menor ou igual a zero.
Para saber os outros valores que não pode ter, temos sempre que prestar atenção no denominador da fração! Esse denominador nunca pode ser zero. Caso contrário, isso levaria a uma divisão por zero e a um problema de conta.
Logo, o denominador de precisa ser diferente de .
.
Para ser dizerente de , tem que ser diferente de zero. Resumindo, não pode ser positivo para não dar problema de cálculo com a raiz quadrada e nem pode valer . Ou seja, só pode ser negativo (menor que zero).
Logo, todos os valores de menores que zero fazem parte do domínio!
Juntando os dois domíniosResumindo, termos o domínio da função é composto pelos valores de e pelos valores de .
Então, domínio de :
Mas calma que o exercício ainda não acabou!
Além de pedir para a gente determinar o domínio, o enunciado também pediu que a gente esboçasse o domínio.
Faremos isso agora!
Passo 4
Primeiro de tudo o que é esboçar o domínio?
Esboçar o domínio é a mesma coisa que pintar a região do plano cartesiano onde todos os pontos doo domínio se encontra.
O plano cartesiano é formado por duas retas: a reta e a reta .
A reta é como se fosse uma régua com todos os valores de do menor para o maior. Os valores de nessa reta crescem da esquerda para a direita. Essa reta é cortada pela reta bem no ponto onde . Ou seja, o lado esquerdo desse ponto de corte tem os valores negativos de . Como os valores negativos de fazem parte do domínio, vamos pintá-lo!
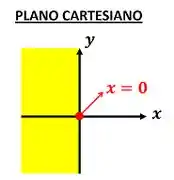
A reta é como se fosse uma régua com todos os valores de do menor para o maior. Os valores de nessa reta crescem de cima pra baixo. Essa reta é cortada pela reta bem no ponto onde . Ou seja, a parte acima desse ponto de corte tem os valores positivos de . Como os valores positivos de fazem parte do domínio, vamos pintá-lo!
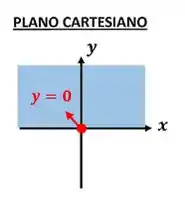
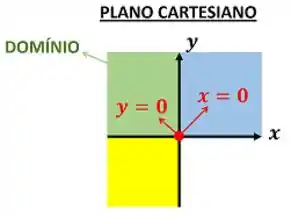
A nossa região do domínio será a que pertence as duas condições ao mesmo tempo. Assim, pintando as duas em um mesmo plano teremos:
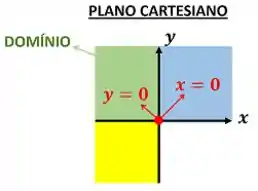
O domínio é a parte que está a esquerda da reta e acima da reta . Portanto, ela é a parte verde do gráfico.
Resposta
Domínio de :
Esboço do domínio: