Esboce o gráfico da curva cuja equação vetorial é dada
a)
Passo 1
Oláá, tudo certinho?
Nesse exercício, queremos esboçar o gráfico dessa função vetorial:
Mas como vamos fazer isso?
Bem, o primeiro passo é lembrar que (uma dimensão), enquanto estamos indo para , que tem duas dimensões
Portanto, a nossa curva vai ter dimensão . Show! Vai ser algo em 3D
Esse algo em 3D que vamos desenhar vai ser assim olha:
Ou seja:
Boaaa, então vamos lá!
Passo 2
No nosso gráfico em 3D vamos ter
Ou seja, primeiramente já temos que a coordenada da curva vale sempre
Ao mesmo tempo, temos que
Onde varia em todos os números reais
Logo, o gráfico que queremos vai ser a intersecção do plano (o plano identidade de para ) com o plano
Passo 3
Nossa superfície vai ser a intersecção desses dois planos:
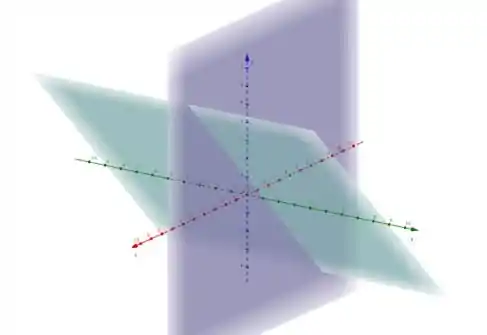
Que é essa reta:
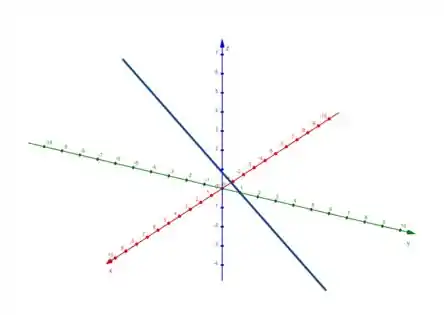
Sucessoooo!
Resposta
Imagem no passo 3