23) (a) Encontre uma matriz não-nula de tamanho tal que .
Passo 1
Oieee, galera linda do Responde Aí. Tudo bem por aí?
Eu não quero ninguém aqui assim:

Quero todo mundo felizãaao, ainda mais depois de resolvermos mais essa! Bora lá então.
Esse exercício nos pede uma matriz não nula com tamanho ( linhas e colunas) que quando encontremos a sua transposta, temos a mesma matriz inicial.
Parece confuso, não é? Mas calma! Esse exercício não tem segredo.
Matrizes transpostas iguais as originais são uma característica das Matrizes Simétricas.
Legal, mas o que são matrizes simétricas?
Passo 2
Vamos considerar a seguinte matriz:
Quando analisamos os termos acima da diagonal principal e os termos abaixo da diagonal principal dessa nossa matriz , é possível perceber que há termos que são iguais. Isso faz com que ela seja conhecida como simétrica exatamente pela simetria da matriz em relação à diagonal principal.
Com cores ficará até mais fácil de ver:
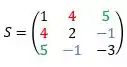
Se encontramos a transposta da nossa matriz , é possível perceber que é igual a .
Veja:
E essa condição satisfaz o nosso enunciado.
Pra essa questão é isso pessoal! Bora pra mais uma?

Resposta
Resposta no desenvolvimento acima.