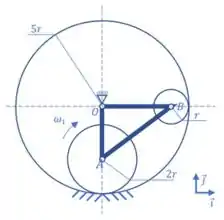
3) A figura ao lado ilustra um mecanismo constituído por um aro fixo de raio e dois discos, um de centro A e raio e outro de centro B e raio , ambos articulados a uma treliça , a qual, por sua vez, é articulada em , centro fixo do aro. O dispositivo assim construído mantém os discos em contato permanente com a superfície interna do aro. Ambos os discos realizam movimento de rolamento sem escorregamento. Sabendo que a velocidade angular do disco de centro A é (constante) e utilizando indicada na figura, pede-se:
a) a velocidade do ponto A.
b) o módulo da velocidade angular do disco de centro B.
c) a velocidade do ponto B.
d) o módulo da velocidade angular da treliça.
e) a aceleração do ponto A.
f) a aceleração do ponto de contato entre o disco de centro A e o aro.
Passo 1
Ooi pessoal, tudo certinho com vocês?
Bora matar mais uma questão de mecânica!
a)
Nesse item é pedido apenas a velocidade do ponto A, centro do disco de raio .
Aqui é bem importante usarmos o fato de que os discos estão realizando movimento de rolamento sem escorregamento, então a velocidade do ponto de contato do disco com o Aro é sempre nula.
Daí, esses pontos vão funcionar como centro instantâneo de rotação para os seus centros.
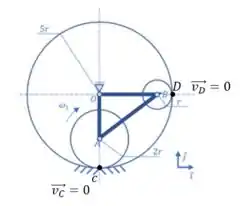
Por isso, podemos escrever que:
Pronto, já matamos a letra a.
Passo 2
b)
Agora, devemos calcular a velocidade angular do disco de centro B e raio .
Temos que ter uma sacadinha, só olhando pro disco e pro aro não sai uma equação que nos ajude a encontrar . Logo vamos olhar pra nossa treliça, mais especificamente para a barra .

Sempre que tiver uma barra envolvida no problema, tem uma equação muito importante que conseguimos escrever. É a equação do vínculo da barra. Ela leva em conta que, como a barra é rígida (ou seja, tem um tamanho fixo), as componentes da velocidade dos pontos da barra na direção precisam ser iguais.
Então, tomando os pontos A e B, vale que:
Para pegar as componentes das velocidades nessa direção, basta multiplicar as suas velocidades absolutas pelo vetor . Daí:
Utilizando o ponto de contato do disco com o aro como um centro instantâneo de rotação para B, podemos escrever que:
Considerando o centro do aro como origem dos eixos, temos que:
Logo:
Boa, conseguimos achar . Vale a pena guardar com carinho essa equação do vínculo da barra gente!
Passo 3
c) Agora, devemos calcular a velocidade de B, centro do disco de raio . Como já sabemos a velocidade angular desse disco, e pelo item anterior também temos uma expressão para em função de , ficamos com:
Prontinho 😊
Passo 4
d)
Nesse item precisamos calcular o módulo da velocidade angular da treliça.
O raciocínio de centro instantâneo de rotação também é bem-vindo nesse caso. Se pararmos pra pensar, como o ponto O é fixo, ele funciona exatamente como um C.I.R para os pontos da treliça. Assim, podemos escrever que:
Onde é a velocidade angular da treliça e é o vetor distância entre a origem e o ponto A. Logo:
Mas, do item a, nós já conhecemos , igualando as duas expressões temos:
Perfeito!
Passo 5
e) Calma pessoal, a questão é longa, mas já tá chegando no fim. E agora vem umas ideias um pouco diferentes. Queremos calcular a aceleração do ponto A, que é o centro do disco de raio . Como tem várias coisas girando nessa questão, precisamos calcular a aceleração de A relativa a algum ponto.
E qual que é o melhor ponto pra gente escolher? Exatamente aquele que está parado Rs, o ponto O. Como ele está parado, essa aceleração já vai ser absoluta, nos poupando um pouquinho de trabalho. Relembrando a nossa fórmula de aceleração relativa, temos que:
Como nessa questão as velocidades angulares são todas constantes, a aceleração angular é nula. Além disso, como já falamos, é um ponto fixo daí . Substituindo os outros dados necessários, chegamos a:
Agora só falta mais uma letra pessoal, não vamos morrer na beira da praia né?! Let’s go!
Passo 6
f)
Finalmente, nesse último item, precisamos calcular a aceleração do ponto . E realmente pessoal, agora que já calculamos a aceleração do ponto A, faz bastante sentido essa pergunta. Porque podemos utilizar um raciocínio igual ao do item anterior, mas agora calculando em relação a A. Daí, usando nossa fórmula para aceleração relativa, vem que:
Bom, novamente como a velocidade angular é constante, temos que . Substituindo os dados já encontrados durante essa pequenina questão, teremos que:
Espero que vocês tenham entendido direitinho, até a próxima pessoal!
Resposta
a)
b)
c)
d)
e)
f)