Num dado instante, o pé A da escada tem aceleração e velocidade , ambas para esquerda. Determine a aceleração do topo e a aceleração angular da escada, nesse instante.
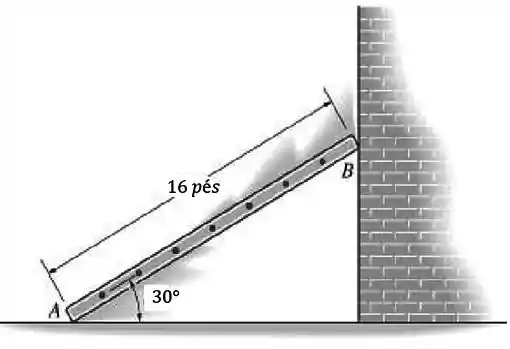
Passo 1
Vamos analisar inicialmente a velocidade do ponto , temos que:
Conforme o ponto vai para a esquerda, o ponto desce. Então, vamos ter que:
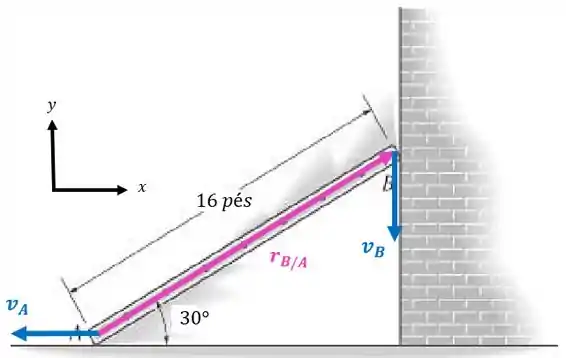
A velocidade será:
E podemos escrever a velocidade do ponto em termos de e :
A decomposição do vetor nos eixos e fica:
Repare que a barra tende a girar em torno do ponto e como este ponto se move para a esquerda, a barra tende a girar no sentido horário:
Então, pela convenção de sinais que adotamos, a velocidade angular desta barra é negativa:
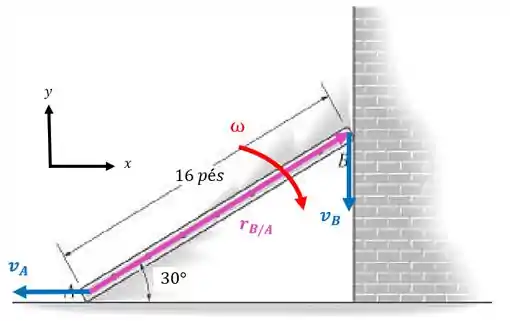
Passo 2
Vamos fazer o produto vetorial agora:
Nossa matriz vai ficar:
Então, o que temos até agora é:
Vamos separar as nossas equações nas componentes e :
Opa, pela primeira equação conseguimos achar o valor da velocidade angular da barra:
Agora podemos achar o valor da velocidade no ponto usando a segunda equação:
Como tudo deu positivo, significa que arbitramos o sentido certo tanto para (sentido horário) quanto para (apontando para o sentido negativo do eixo ).
Passo 3
Agora vamos analisar as acelerações:
Repare que a aceleração do ponto será no mesmo sentido da velocidade, pois não está acontecendo uma desaceleração:
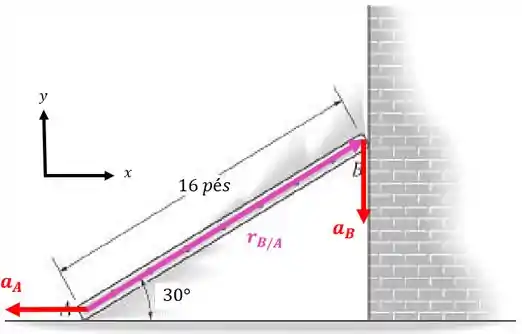
Temos que a aceleração do ponto é:
E a aceleração do ponto pode ser escrita assim:
Então, como fica a nossa equação:
Vamos ter que:
Repare que a aceleração angular da barra aponta no sentido horário também, assim como a velocidade angular. Isso porque a barra não sofre desaceleração:
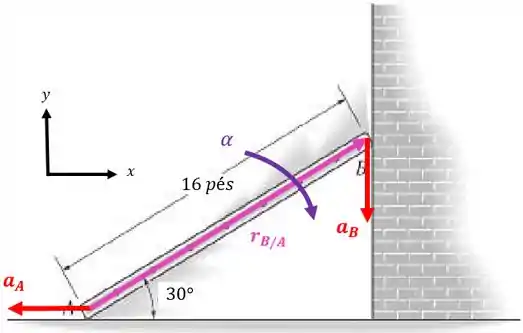
Então, podemos escrever a aceleração angular em função das suas componentes:
Vamos fazer o produto vetorial:
Vamos substituir isso na nossa equação da aceleração:
Agora, vamos separar nossa equação nas componentes e :
Da primeira equação conseguimos achar o valor da velocidade angular:
E substituindo isso na segunda equação obtemos o valor da aceleração do ponto :
O sinal positivo que achamos tanto para a aceleração angular quanto para a aceleração do ponto indica que arbitramos o sentido correto para esses vetores.