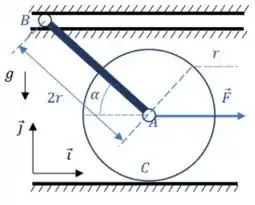
03) O disco homogêneo de centro , raio e massa é articulado em e uma barra homogênea esbelta , de massa , comprimento e inclinada de um ângulo em relação à horizontal, tendo sua outra extremidade ligada a um rolete guiado por uma guia horizontal, conforme ilustrado na figura. Sob a ação de uma força horizontal de módulo constante , o disco rola escorregar sobre um plano horizontal. Desprezando o atrito no contato entre o rolete e a guia horizontal, pede-se:

a) A aceleração angular do disco.

b) As magnitudes das componentes da reação em .

c) As magnitudes das componentes da força vincular em .

d) As magnitudes das componentes da reação em .

e) O valor mínimo do coeficiente de atrito entre o disco e a pista para que o disco não escorregue.

a) Nesse primeiro item devemos determinar a aceleração angular do disco.

Mas ó, praticamente não temos informações cinemáticas, a melhor opção é partir pros nossos teoremas que relacionam as forças, ou seja, o teorema da Resultante e o Teorema da quantidade de momento angular (TQMA).

Antes de escrever as equações, bora desenhar o diagrama de corpo livre da barra e do disco, beleza?

Começando pelo disco, sabemos que nele atua a força peso, a força e a reação vincular da barra no seu centro, . Além disso, no ponto de contato com a superfície, , também atuam a normal e a força de atrito. Assim, podemos desenhar:

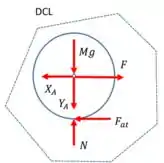
Já na barra, temos as reações vinculares em no sentido oposto ao desenhado no DCL do disco (devido ao equilíbrio do nó ). Temos também o peso da barra, , agindo no seu centro, bem como a reação da articulação em . Logo:

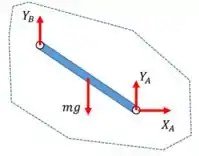
Muito bom!

Agora que já temos os DCL’s fica mais tranquilo de usar os teoremas. Então, começando pela barra temos:

Teorema da Resultante:

Puts, mas e quanto que valem essas componentes?

Tem uma sacada muito legal aqui galera.

É tipo um vínculo geométrico, como a barra possui tamanho fixo e liga o rolete e o disco, ambos se movimentando sempre na direção , a barra também está se movimentando nessa direção! Logo:

Substituindo esse resultado no teorema da resultante, nós temos que:

Boa! Escrevendo agora o TQMA para a barra, com polo no seu centro , vem:

Como a barra apenas translada, vem:

Ok! É a vez do disco.

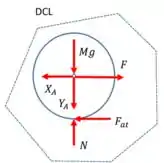
Aplicando o teorema da Resultante, vem:

Já pelo TQMA, com o polo em , temos:

Bouaa!

Pra finalizar essa parte, é bom lembrarmos que pelo vínculo geométrico da barra e do disco, eles devem ter a mesma aceleração de translação. Ou seja:

Além disso, o ponto é como um centro instantâneo de rotação, assim:

Agora que já temos um monteee de equações, bora montar um sisteminha:

Massa, temos variáveis e também equações 😊

É só descer a mão nas contas!

Substituindo e em , vem:

Aee, finalmente achamos a aceleração angular do disco 😊

b) Devemos determinar a magnitude das reações, em e em , no ponto . Ou seja, devemos determinar os valores de e de . Reescrevendo nosso sistema:

Da equação , sabemos que:

Substituindo o resultado do item anterior, , vem:

Pra calcular a normal, precisamos calcular . Para isso, substituído em , vem:

Isolando , vem:

Substituindo o valor encontrado para , temos:

Substituindo esse resultado em temos que:

Prontinho, determinamos as reações em C 😊

c) Vamo calcular agora as reações vinculares em , ou seja, e .

Pelo item anterior, temos:

Já calculamos no item anterior, logo:

d) Em , como ela é guiada horizontalmente, temos apenas a reação .

Da equação do sistema, temos:

e) Estamos quase acabando galera. Pra finalizar precisamos determinar o valor mínimo do coeficiente de atrito , de modo que não haja escorregamento.

Para que não haja escorregamento, basta que a força de atrito seja a que encontramos anteriormente. Ou seja:

Mas, sabemos que sempre vale:

Ou seja, o menor valor possível de é justamente na igualdade:

Substituindo esses valores, chegamos que:

E é issooo!! Matamos mais uma questãozinha!

Espero que vocês tenham entendido bem direitinho, até a próxima pessoal 😉