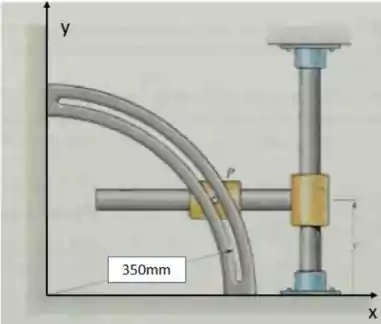
01) Na figura mostrada, temos o ponto P descrevendo uma trajetória circular. Por isso, observe que os movimentos em e estão relacionados.
Se o movimento em é dado por , pede-se, para o instante
a) as velocidades e acelerações do ponto , em coordenadas retangulares;
b) as velocidades e acelerações do ponto em coordenadas ;
c) o raio de curvatura da trajetória de .
Passo 1
Faaaaala galerinha do Responde Aí, tudo certo com vocês?
Bora matar mais uma questãozinha de mecânica!
a) Pra começar, temos uma estrutura na qual o ponto realiza uma rotação em torno da origem do sistema de coordenadas retangulares. Precisamos determinar a velocidade e aceleração do ponto nesse tipo de coordenadas quando .
O que é legal, é que já foi dada a posição do ponto . Assim, já podemos calcular e , pois:
Show, então quando ficamos com:
Beleza, a primeira parte já foi. Precisamos agora calcular e .
O que é muito importante ficarmos atentos nessa questão, é que o ponto descreve uma trajetória circular, cuja circunferência está centrada em e possui raio . Daí, a equação dessa circunferência, vale:
Usando a equação de em função do tempo na expressão acima, também vamos ter em função do tempo. Daí, pra encontrar a velocidade e aceleração, basta derivarmos, bem semelhante ao que fizemos para e .
Como queremos saber apenas , podemos substituir na expressão acima. Usando que:
Logo:
Agora vai dar um trabalhinho algébrico, que inclusive é um dos motivos das coordenadas retangulares não serem tão indicadas para esse tipo de movimento, mas bora lá, sem preguiça haha. Lembrando que aqui é necessário utilizar a regra da cadeira e do produto:
Beleza, com cuidado pra não errar continhas, vamos calcular a derivada desses dois termos:
Top, substituindo na nossa equação vem que:
Estamos quase lá. Como queremos saber apenas a aceleração em , não precisamos ter o trabalho algébrico de abrir essa expressão toda, podemos só substituir os valores de:
Massa! Substituindo esses dados todos em para , vem que:
Fazendo todas essas continhas, finalmente chegamos que:
Excelente! Agora é só finalizarmos a questão, escrevendo a velocidade e aceleração resultante em termos das suas componentes:
Prontinho 😊
Passo 2
b) Nesse item também nos é pedido a velocidade e aceleração do ponto em , mas agora em coordenadas normal e tangencial . O importante de lembrarmos é que no movimento circular a velocidade é sempre tangencial (a componente normal da velocidade é nula). Daí, podemos escrevê-la como:
Onde é o versor na direção tangencial da trajetória.
A dica aqui pessoal é usarmos os resultados já encontrados no item A. Por esse item, nós já conhecemos o vetor velocidade em , precisamos apenas reescrevê-lo. Pois sabemos que:
Logo, o módulo vale:
Portanto:
Show galera, já foi uma parte. Bora pra aceleração.
Lembra que em coordenadas n-t, a aceleração pode ser escrita como:
Onde é o raio de curvatura.
Pra descobrir cada uma dessas componentes, podemos fazer os produtos escalares e .
O versor pode ser encontrado pela direção da velocidade. Então:
Como, do item A, temos:
Fazendo o produto escalar, chegamos que:
Já o versor pode ser encontrado através das coordenadas da posição .
Daí é só usar um pouquinho de conhecimento de álgebra linear:
Boa pessoal! Vamos calcular o outro produto escalar:
Excelente! Agora que já calculamos as duas componentes, é só reescrever:
Aee, já foi outra letra, falta só mais uma. Vamoo!!
Passo 3
c) Nesse último item precisamos calcular o raio de curvatura da trajetória. Podemos olhar para a figura, que nos mostra que o raio é de , ou podemos também analisar a componente normal da aceleração.
Isso porque:
Aeee, terminamos a questão. Vocês conseguiram entender direitinho? Essa foi boa para revisar as coordenadas n-t.
Resposta
a)
b)
c)