Num dado instante, o volante está girando com a velocidade e a aceleração angulares indicadas na figura. Determine a aceleração do bloco , nesse instante.
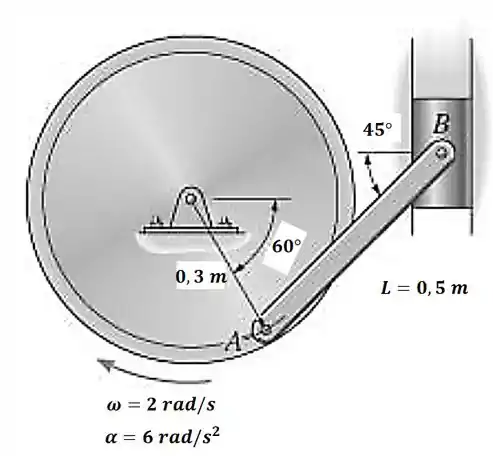
Passo 1
O que queremos saber é a aceleração do ponto , então vamos escrever a nossa equação da aceleração relativa assim:
Repare que não sabemos a aceleração angular da barra , mas podemos usar a equação da velocidade do ponto para achá-la:
A posição é:
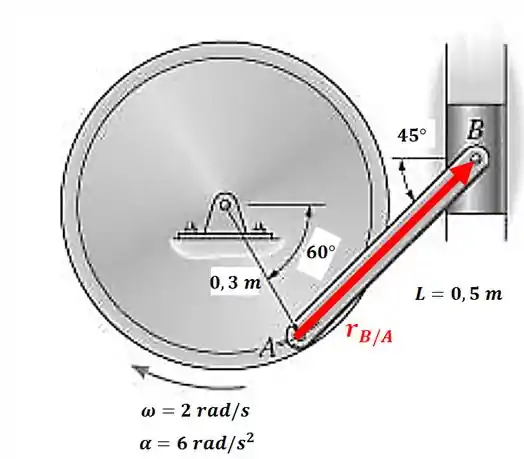
A velocidade do ponto podemos achar pela equação:
A velocidade angular do volante é negativa, pois está girando no sentido horário:
E a posição do ponto com relação ao centro do volante é:
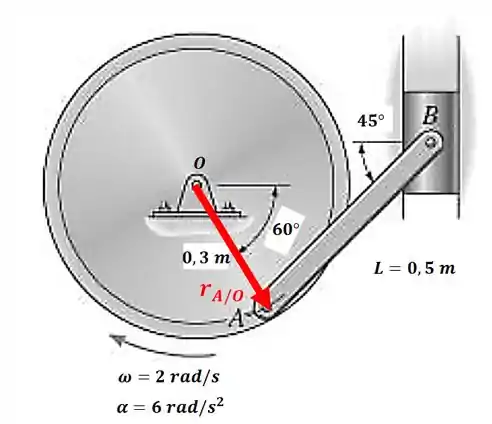
Então, a velocidade do ponto será:
Resolvendo esse produto vetorial temos:
Passo 2
Agora sim podemos achar o valor da velocidade angular da barra usando a equação da velocidade do ponto :
Repare que o ponto só pode se mover no eixo , então vamos arbitrar a velocidade como positiva:
E vamos arbitrar o sentido da velocidade angular da barra como positivo:
Então, o produto vetorial fica:
Substituindo isso na nossa equação:
Agora vamos somar os termos de mesma componente:
Da equação em podemos achar o valor de :
Como o resultado deu negativo, significa que arbitramos o sentido contrário:
Como não vamos precisar do valor de , vamos deixa-lo pra lá!
Passo 3
O que queremos saber é a aceleração do ponto , certo? Então, vamos resgatar a equação lá do início:
Vamos substituir o que já temos:
Ou seja, precisamos achar a aceleração do ponto e a aceleração angular da barra .
Vamos começar pela aceleração do ponto :
Sabemos que a velocidade angular do volante é negativa, pois está girando no sentido horário:
Então:
Resolvendo o produto vetorial temos:
Substituindo isso vamos ter:
E a aceleração angular da barra vamos arbitrar como positiva:
Passo 4
Agora vamos substituir essas coisas na equação da aceleração do ponto :
Repare que o ponto só pode se mover na vertical, então a sua aceleração é:
Vamos arbitrar como positiva!
Então, vamos ter que:
Vamos resolver o produto vetorial:
Substituindo isso aí na nossa equação:
Agora vamos separar as componentes:
Da primeira equação podemos determinar o valor de :
E finalmente podemos achar o valor da aceleração do ponto :
Então: