02) Um disco de massa , raio e centro , rola sem deslizar sobre um plano inclinado, sendo o ponto de contato. O disco é tracionado por um cabo inextensível, de massa desprezível, ligado por meio de uma polia a um bloco de massa . No instante inicial, o sistema está em repouso e Sabendo que a polia de centro tem massa desprezível, pede-se, para o instante ilustrado na figura:
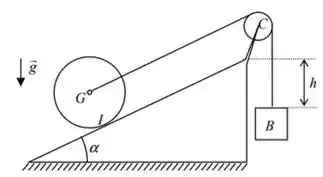
a) a energia cinética do sistema;
b) a velocidade e a aceleração do bloco em função de
c) a tração no cabo e as componentes normal e tangencial da força de contato no disco.
Passo 1
Ooii pessoal, tudo bem com vocês?
Nessa questão temos uma situação bem clássica. Um disco, sob um plano inclinado, está preso a um fio tracionado por uma carga .
a) Pra começar a brincadeira, devemos calcular a energia cinética do sistema (disco+bloco).
Aqui, o que pode gerar certa dúvida, é a influência do movimento de rotação do disco na energia cinética do sistema. Será que altera a energia ou podemos ignorar a rotação?

Então, sempre que tem rotação precisamos acrescentar uma parcela a mais na energia cinética:
Assim, considerando também as parcelas de translação do disco e do bloco , temos:
Mas, como o fio é inextensível, podemos afirmar que:
Além disso, como o disco rola sem deslizar, o ponto de contato é como um CIR para o disco. Assim, também podemos afirmar que:
Por último, como trata-se de um disco, sabemos também que:
Substituindo todas essas informações na expressão da energia cinética, temos:
Logo:
Bouaaa! O primeiro item já foi 😊
Passo 2
b) Agora devemos calcular a velocidade e aceleração do ponto em função de .
Pô, pensa comigo, se precisamos que a resposta esteja em função de altura , tentar resolver usando os teoremas que envolvem força não é uma ideia muito boa.
Bora partir pra energia!

Aplicando o teorema da energia cinética ao nosso sistema, do instante inicial até o instante mostrado, temos que:
Vamos pensar agora em quais forças estão realizando trabalho.
A força normal de contato entre o disco e o plano inclinado não realiza trabalho, ela é sempre perpendicular ao deslocamento.
A força de atrito também não realiza, pois o disco rola sem deslizar, assim a velocidade do ponto de contato é nula a cada instante. A tração é uma força interna, logo não realiza trabalho.
Portanto, as únicas forças que realizarão trabalho é a força peso no bloco e a sua componente perpendicular ao plano inclinado no disco.
Como no instante inicial o sistema está em repouso, temos:
Igualando as duas expressões, temos:
Logo:
Como vimos no item anterior, vale que:
Como o bloco está descendo, ou seja, no sentido , temos:
Bouaaa! Pra encontrar a aceleração, basta derivarmos :
Tirando tudo que é constante da jogada, ficamos com:
Mas,
Substituindo, temos:
Daí, temos:
Como o bloco movimenta-se na direção , temos:
Excelentee!! Entenderam bem?!
Vamo simbora!!
Passo 3
c) Aqui devemos determinar a tração no fio além das componentes de da reação de contato entre o disco e o plano inclinado.
Como já sabemos a aceleração do bloco e do disco, podemos agora partir pra uma análise de forças.
Para o bloco atuam apenas a tração e a força peso, montando a equação de forças temos:
Substituindo o valor de , temos:
Logo:
Já no disco atuam o atrito e a normal no ponto de contato , além da tração e da força peso. Logo:
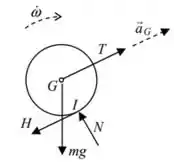
Montando as equações de força na direção tangencial e perpendicular ao plano inclinado, temos:
Daí, logo de cara temos:
Massa!
Pra descobrir basta substituir o valor de e lembrar que . Assim:
Aeeee, terminamos! Conseguiram entender bem as ideias da questão?
É isso galera, espero vocês na próxima. Tamo junto! 😉
Resposta
a)
b)
c)