03) As barras , de massa e , de massa , são articuladas entre si no ponto , conforme mostrado na figura. A extremidade da barra é vinculada a uma parede vertical por meio de uma articulação. A extremidade da barra é apoiada em uma superfície horizontal isenta de atrito. Admitindo que as barras se encontrem inicialmente em repouso na configura indicada na figura, pede-se, para o instante em que o sistema inicia o seu movimento:
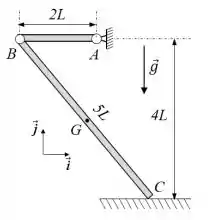
a) Os diagramas de corpo livre das barras e ;
b) a relação entre as acelerações angulares e das barras e , respectivamente;
c) a aceleração do centro de massa da barra em função da aceleração angular ;
d) as acelerações angulares e das barras em função dos parâmetros dados;
e) a reação na extremidade da barra .
Dado:
Passo 1
Eaí galerinha, tudo certo com vocês?
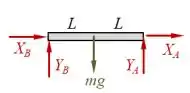
a) Nesse exercício, como é bem comum nas questões de mecânica, devemos começar desenhando o diagrama de corpo livre (DCL) das barras e .
Já sabe qual a dica master pra desenhar DCL?

A dica é sempre começar identificando as forças que agem em cada peça.
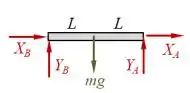
Na barra , por exemplo, temos o peso atuando no meio da barra, além de articulações nos nós e , gerando uma reação vertical (em ) e outra horizontal (em ) em cada um desses nós.
Daí, lembrando que podemos chutar o sentido inicial das reações, é só colocar isso tudo num desenho:
Já para a barra , como o nó precisa estar em equilíbrio, deve estar agindo em forças de igual módulo, direção, mas sentido oposto a e . Além disso, como a barra apoia-se sobre o solo, há uma reação vertical em . Temos também o peso agindo no meio da barra. Assim:
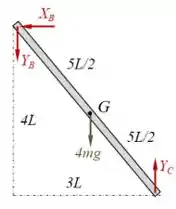
Boaaa galera!
Passo 2
b) Nesse item devemos determinar a relação entre as acelerações angulares das barras e , ou seja, a razão entre e .
É difícil logo de cara conseguir ver uma equação que relacione as duas acelerações angulares, mas tem uma sacada que pode ajudar muito! Vou dar uma dica, tem a ver com ...

A questão fala que está apoiado na superfície, logo, quando a barra começar a se movimentar vai apenas deslizar na horizontal. Ou seja, todo seu movimento se dá nesse eixo. Assim:
Essa equação é legal porque agora, podemos tentar escrever envolvendo e , sabendo que disso duas equações escalares. ( variáveis, equações, perfeito...).
Como queremos relacionar as duas acelerações angulares, podemos escrever como:
Como está fixo no apoio, ele funciona como centro instantâneo de rotação para , logo:
Além disso,
Substituindo esses dois resultados em , vem:
Daí, como , surgem duas equações escalares:
Assim, finalmente encontramos:
Prontinho 😊
Passo 3
c) Aqui devemos calcular a aceleração do centro de massa da barra em função de .
Uma boa ideia é já usar a equação da aceleração no movimento plano geral e escrever que:
O massa de usar essa equação é que, pelo enunciado da questão, estamos interessados no instante em que o sistema inicia o seu movimento (partindo do repouso), ou seja, .
Isso simplifica um bocado as continhas!!
Do item b), sabemos que:
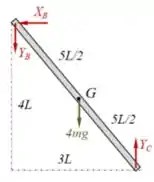
Além disso, da figura abaixo podemos concluir que:
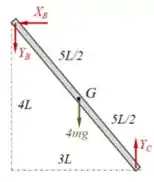
Substituindo, vem:
Logo:
Excelente!
Passo 4
d) O objetivo agora é calcular e .
Pensa comigo, nos itens anteriores já usamos muitas equações da cinemática das acelerações, mas ficamos sempre em função de ou .
Além disso, um dos dados da questão foi o momento de inércia da barra no seu centro geométrico.
Isso tudo tá querendo nos dizer alguma coisa...
Qual teorema a gente pode usar que envolve o momento de inércia?

É justamente o teorema da quantidade de momento angular, o TQMA!
Aplicando o TQMA para a barra , usando como polo, temos:
Mas, lembra que é um ponto fixo, assim . Olhando também para o DCL de podemos calcular o momento resultante em , daí:
Só que, pelo teorema dos eixos paralelos sabemos:
Substituindo, temos:
Fazendo , vem:
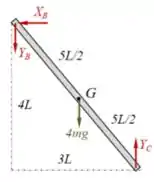
Top! Aplicando o mesmo teorema, mas agora para o polo da barra BC, vem:
Passo 5
Puts, esse negócio tá complicado né? Temos mais variáveis do que equações...

Mas ainda tem um teorema legal que podemos usar: o teorema da resultante! Aplicando-o para a barra , temos:
Como do item c temos:
Vem que:
De , vem:
Substituindo em , vem:
Substituindo tais resultados em , vem:
Portanto, usando aquela relação lá do comecinho:
Excelente galera, estamos quase acabando 😊
Passo 6
e) Por último, devemos calcular .
Do item anterior, temos como função de , dado por:
Substituindo, vem:
Ufaaa! Essa questão era complicadinha né galera. Bora dar uma descansada pra depois voltar com tudo!! Até a próxima, gentee!
Resposta
a) Resolução no texto.
b)
c)
d)
e)