03) No mecanismo a seguir, no instante mostrado, a barra AB possui velocidade angular de e aceleração angular de , ambas no sentido anti-horário. Nesse instante, a barra BC gira com a mesma velocidade angular da barra AB enquanto a barra CE gira com velocidade angular no sentido horário.
Pede-se:
a) Calcule a aceleração angular da barra BC;
b) Calcule a aceleração do ponto E.
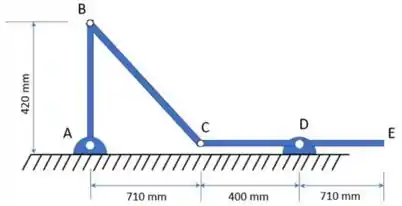
Passo 1
Faaala galerinha, tudo bom?
a) Nesse item é pedido pra gente calcular a aceleração angular da barra BC. Como sabemos pelo enunciado, BC está girando no sentido anti-horário com uma aceleração angular .
Precisamos pensar em alguma equação da mecânica que envolva .

Uma boa ideia é usarmos a expressão da aceleração em um movimento plano geral para o ponto B, pois sabemos que:
(1)
Beleza, pelos dados da questão, na equação acima ainda não conhecemos os valores de e . Então, vamos por partes determinando algumas dessas variáveis até sermos capazes de resolver essa equação encontrando .
A aceleração de B pode ser vista olhando para a barra AB, lembrando que A é um ponto fixo (, daí:
Massa! Pela figura, considerando a origem do plano cartesiano em A, temos que:
Já a aceleração de C, podemos usar também a equação do movimento plano geral, mas agora em relação a D (que também é um ponto fixo, logo ).
Também pela figura, temos que:
Substituindo:
Pronto, substituindo (2), (3) e (4) em (1), vamos ficar com:
Top!! Mesmo que ainda tenhamos duas variáveis, não tem problema. Equações vetoriais como essas sempre nos dão um sisteminha com uma equação para cada eixo cartesiano (.
Então vamos resolver o produto vetorial que tá aparecendo aí pra depois escrever a equação vetorial bonitinha.
Show, voltando na nossa equação principal teremos:
Só organizando um pouco, ficamos com:
Separando em um sisteminha de duas equações, temos:
Como nesse item só queremos descobrir , bora resolver apenas a primeira equação:
(sentido anti-horário)
Ufaaa! Deu um trabalhinho, mas achamos. Bora pra próxima!
Passo 2
b) Aqui devemos encontrar a aceleração do ponto E.
Beleza! A forma mais fácil de escrever a aceleração do ponto E é usar D como referência, pois ele é um ponto fixo. Daí:
Precisamos determinar alguns termos dessa equação. Começando pela aceleração angular da barra CE, podemos usar o sisteminha final do item A (mais precisamente a segunda equação).
Massa! Pela figura também temos que:
Show! Voltando na nossa equação principal, temos:
Uhuuul! Conseguimos! É isso aí pessoal, a ideia principal dessa questão é saber utilizar a expressão da aceleração em um movimento plano geral. Espero que vocês tenham entendido bem direitinho.Até a próxima! 😉
Resposta
a)
b)