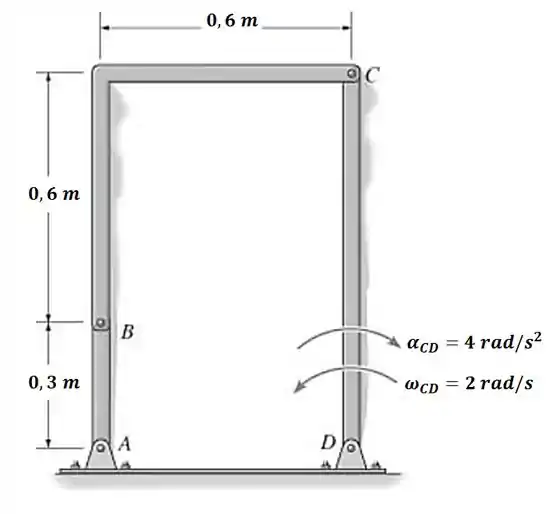
Determine a aceleração angular da barra de ligação , considerando que a barra tem a velocidade e a desaceleração angulares indicadas na figura.
Passo 1
Vamos começar resolvendo esta questão pela barra , pois temos alguma informação sobre seu movimento. Repare que o ponto realiza um movimento em torno do ponto que está fixo, então podemos dizer que:
Sabemos que a barra possui uma desaceleração, então:
Já a sua velocidade angular é positiva, pois está girando no sentido horário:
E o vetor posição ?
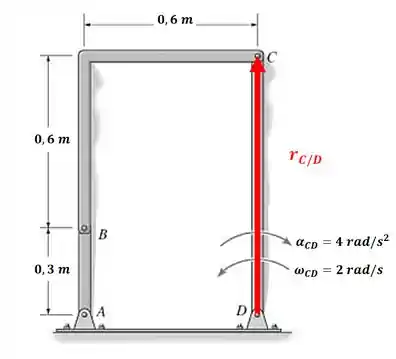
Então:
Agora que identificamos cada termo da nossa equação, é só substituirmos tudo:
Vamos resolver este produto vetorial:
Então:
Passo 2
Agora vamos achar a velocidade do ponto :
Repare que o ponto está fixo, então sua velocidade é nula:
Portanto:
Resolvendo este produto vetorial, vamos ter que:
Repare que o produto vetorial de uma componente em e outra em sempre resulta em uma componente em . ![]()
Passo 3
Vamos partir para a barra . Repare que o ponto gira em torno do ponto que está fixo, então:
Como o ponto é fixo, sua velocidade é nula:
A velocidade angular da barra nós não sabemos, mas vamos arbitrar que ela esteja no sentido positivo:
E o vetor posição ?
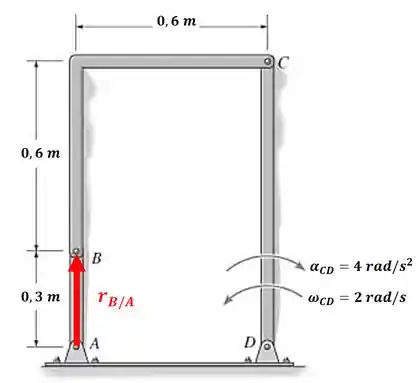
Como já definimos o que é cada termo da nossa equação, vamos substituir as coisas:
Resolvendo este produto vetorial, vamos ter que:
Vamos guardar esta informação e tentar outra maneira de achar a velocidade do ponto .
Passo 4
Agora vamos relacionar os pontos e para acharmos a velocidade do ponto , já que temos informações sobre o ponto :
Vamos identificar o que é cada termo desta equação.
A velocidade do ponto nós já calculamos:
A velocidade angular da barra nós não sabemos, mas vamos arbitrar como positiva:
E o vetor posição relativa será:
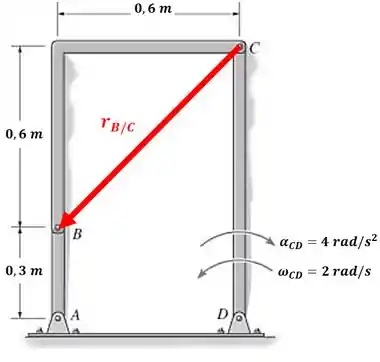
Pronto! Agora é só substituir:
Resolvendo este produto vetorial:
Então, vamos ter que:
Beleza?
Lembra que eu falei para guardarmos a informação que tínhamos sobre a velocidade do ponto ? Vamos resgatá-la agora:
E substituir ela na nossa equação:
Agora vamos separar as equações de acordo com as componentes e :
Da equação em tiramos que a velocidade angular da barra é zero:
E da primeira equação, temos que:
Como a velocidade angular da barra deu positiva, significa que arbitramos o sentido correto para ela:
Passo 5
Agora vamos relacionar o ponto e para achar a aceleração. Como esses dois pontos se movem, temos que:
O que não sabemos dessa equação é a aceleração do ponto () e a aceleração angular da barra . Vamos arbitrar o sentido positivo para a aceleração angular da barra :
Pronto! Vamos substituir tudo o que temos:
Não esqueça que a velocidade angular da barra é zero!
Vamos resolver o produto vetorial:
Substituindo na nossa equação, temos que:
Vamos guardar essa informação e arranjar outro jeito de achar a aceleração do ponto !
Passo 6
Outra forma de achar a aceleração do ponto é usando a barra . Como o ponto gira em torno de um ponto fixo (ponto ) vamos ter que:
Nós já determinamos antes que:
E:
Falta a aceleração angular da barra () e é exatamente isto que a questão quer saber!
Vamos arbitrar o sentido positivo para ela:
E agora podemos substituir tudo:
Como já estamos craques em produto vetorial, vamos ter que:
Então, a nossa equação fica:
Lembra o que sabemos sobre aceleração do ponto ?
Vamos substituir isso na nossa equação lá de cima:
Agora é só separarmos as equações de acordo com as componentes e :
Resolvendo a segunda equação, temos que:
Substituindo isso na primeira equação temos que:
Como achamos um valor negativo para a aceleração angular da barra , significa que arbitramos o sentido contrário para ela. Então, ela está girando no sentido horário: