03) Um disco homogêneo move-se sobre uma pista plana horizontal sob a ação de uma força passante pelo seu centro de massa. O coeficiente de atrito cinético entre as superfícies do disco e da pista é . Supondo-se que o movimento do disco seja de rolamento sem deslizamento, pede-se:
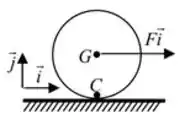
a) Desenhar o diagrama de corpo livre do disco;
b) determinar a aceleração angular do disco e a aceleração do seu centro de massa;
c) determinar as componentes horizontal e vertical da força de contato entre o disco e a pista;
d) estabelecer a condição que deve ser satisfeita para que o movimento hipoteticamente realizado pelo disco – rolamento sem deslizamento – seja possível.
Passo 1
Eaí gente! Tudo certinho com vocês?
a) Pra começar mais uma questão de mecânica precisamos desenhar o diagrama de corpo livre (DCL) do disco. O primeiro passo nesses itens de fazer o DCL é sempre identificar as forças que estão agindo no corpo.
No caso do nosso disco, temos além da força , há a força peso atuando em G e as forças Normal e de atrito agindo no contato do disco com o solo. Daí, temos:
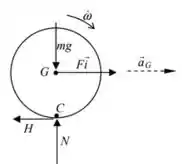
Passo 2
b) Beleza, aqui devemos determinar a aceleração angular e a do centro de massa do disco. Pensa comigo, se temos várias forças atuando em um corpo e queremos a aceleração, temos que invocar nossos teoremas que envolvem força e momento: O Teorema da Resultante e o Teorema da quantidade de movimento angular (TQMA).
Pelo TQMA:
Daí:
Massa! Agora podemos usar as equações cinemáticas pra relacionar a aceleração angular e a linear.
Como o disco rola sem escorregar, vale que:
Pensando no centro de massa, a trajetória dele é uma linha reta, ou seja, ele faz um movimento retilíneo paralelo à superfície. Assim, podemos afirmar que:
Passo 3
c) Nesse item só precisamos determinar as forças de atrito e normal . Vamos então usar o nosso outro teorema.
Pelo teorema da resultante, podemos escrever:
Daí, vem direto que:
Boa! Agora só falta o último item!
Passo 4
d) Precisamos calcular a condição matemática para que esse movimento, rolamento sem deslizamento, seja realmente possível.
O ponto é que de acordou com o que a gente propôs na resolução da questão, tem uma força que precisa obedecer a uma certa condição para que possa existir. É justamente a força de atrito, lembra que:
Então, substituindo a expressão que encontramos pra força de atrito, vamos ter:
Essa é a nossa condição. Se uma força maior do que esse valor for aplicada no nosso disco, não teremos um movimento com rolamento sem deslizamento. Sacaram a ideia?
É isso galera! Matamos mais uma questãozinha de mec. Espero que vocês tenham gostado, até a próxima 😉
Resposta
a) Resolução no texto.
b)
c)
d)