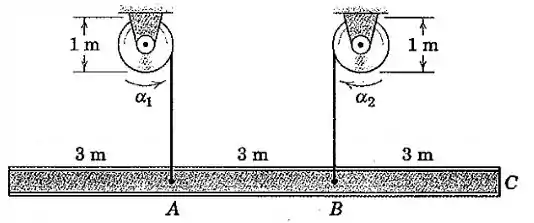
A viga de aço de está sendo levantada a partir de sua posição horizontal pelos dois cabos presos em e . Se as acelerações angulares iniciais dos tambores de elevação são e nos sentidos indicados, determine a aceleração angular correspondente da viga, a aceleração de , e a distância desde até um ponto sobre a linha de centro da viga que não possui aceleração.
Passo 1
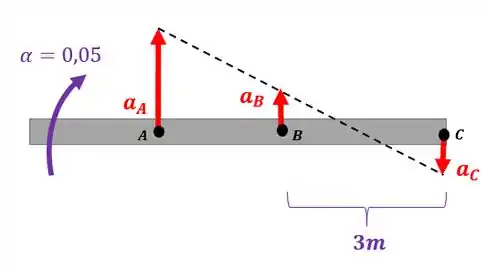
Vamos começar montando um esquema para entendermos o que está acontecendo:
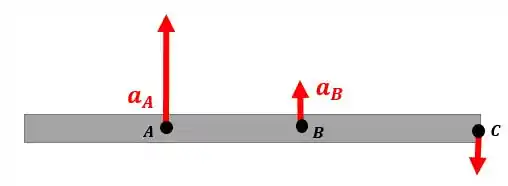
Repare que o ponto é puxado com uma velocidade maior que o ponto . Mas quando isso acontece o ponto acaba descendo, pois a viga tende a girar em torno do ponto que vamos chamar de :
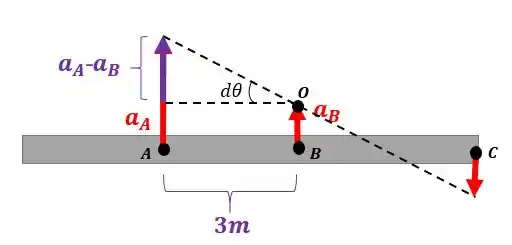
Podemos calcular a aceleração dos pontos e com os dados das suas respectivas polias:
E para o ponto :
Agora podemos achar a aceleração relativa de com relação a :
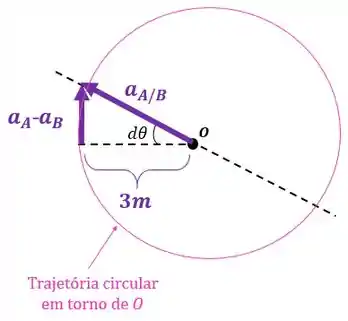
Repare que a viga tende a girar no sentido horário, então a aceleração angular é negativa (não esqueça da nossa convenção de positivo e negativo):
Passo 2
Como estamos analisando o movimento em torno de e sabemos que a viga gira com aceleração angular de , podemos calcular a aceleração do ponto usando nosso esquema:
Vamos ter que:
Como est�� em sentido contrário a , temos que colocar um sinal negativo:
Repare que o sinal deu positivo, o que indica que o sinal que arbitramos para está correto, ou seja, ele aponta para baixo:
Passo 3
A questão pede a distância do ponto até um ponto de aceleração nula que passe pela linha de centro da viga:
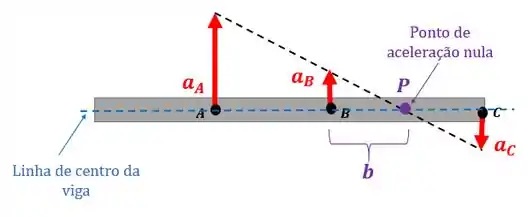
Para achar a distância é só usarmos o nosso esquema:
Sabemos que a aceleração no ponto é zero, então: