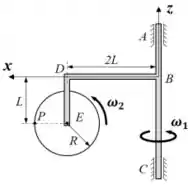
02) A peça gira em torno do eixo vertical com velocidade angular constante , transportando em sua extremidade um disco de raio , o qual, por sua vez, gira com velocidade angular ( constante) em relação à peça . Utilizando o sistema de referência , solidário à peça , e considerando o instante ilustrado na figura, determine:
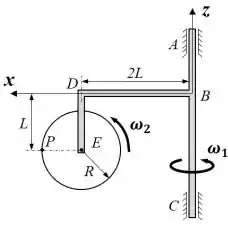
a) o vetor rotação absoluta do disco;
b) o vetor aceleração rotacional absoluta do disco;
c) as velocidades relativa, de arrastamento e absoluta do ponto do disco.
d) as acelerações relativas, de arrastamento, de Coriolis e absoluta do ponto do disco.
Passo 1
Faaala galera, tudo bom com vocês?
a) Nesse exercício temos um problema bem recorrente em mecânica: um disco que gira em torno do eixo , acoplado a uma peça que gira em torno do eixo .
No item a) precisamos determinar o vetor rotação absoluta do disco, vocês lembram o que é esse vetor?

Basicamente, ele é o vetor resultante das rotações realizadas pelo corpo, sacou?
Então, se o nosso disco realiza rotação em torno de dois eixos, o vetor resultante da rotação deve ser a soma da componente em cada um dos eixos. Logo:
Prontinho, bem simples né?
Passo 2
b) Já nesse item precisamos determinar o vetor aceleração rotacional do disco. Aqui, o conceito de aceleração rotacional é um pouquinho diferente.

Ele também tem a mesma ideia de aceleração resultante de rotação para um corpo que gira em mais de um eixo. Porém é muito importante lembrar que, em casos como esse, surge a aceleração de Coriolis, e aí precisamos considerá-la também no cálculo da aceleração rotacional.
Como as velocidades angulares do disco e da estrutura são constantes, temos:
Logo:
Muito bom! Pegaram a ideia?
Passo 3
c) Agora vamos passar a analisar o ponto do disco.
Pra começar, devemos determinar a velocidade absoluta, relativa e de arrastamento de .
Beleza, mas e como é que faz isso?

Bom, é que uma ideia muito recorrente em mecânica é imaginarmos o movimento do corpo como a composição de dois movimentos:
- Movimento em relação a um ponto do próprio corpo. Por exemplo, no caso dessa questão, podemos imaginar o movimento de em relação a , o centro do disco.
- Movimento em relação a um referencial fora do corpo, e que enxerga o movimento do ponto que coincide com no instante considerado. Isso é basicamente pra, nesse caso por exemplo, a gente olhar apenas a influência da rotação de no movimento de , tão ligados?
Ou seja, resumindo tudo, dividimos o movimento na parcelada devida à rotação do disco (relativa) e na parcela devida à rotação da estrutura (arrastamento). Daí, podemos escrever:
Em relação a , é claro que o próprio ponto está parado. Além disso, no instante considerado na figura do enunciado, temos:
Show, daí temos:
Massa!
Bora calcular agora e depois .
Pra calcular a velocidade de arrastamento, podemos imaginar o movimento do ponto que coincide com (igual falamos ali em cima) em relação a um referencial em , por exemplo. Daí:
Lembrando que
Substituindo, temos:
Excelente! Pra finalizar esse item, bora calcular , que é basicamente:
Prontinho! Falta só mais um item, vamo simboraaaa!
Passo 4
d) No último item precisamos calcular a aceleração relativa, de arrastamento, de coriolis e absoluta do ponto .
Como vimos no item c), pra calcular a aceleração relativa podemos tomar o ponto como referência. Daí:
Como e , temos:
Pensando agora na aceleração de arrastamento, podemos novamente tomar o ponto como referência. Logo:
Mas lembra que estamos fazendo tudo em relação a B, logo . Além disso, é constante, o que implica em . Daí:
Top! Será que agora é só somar os dois resultados pra achar ?
Nãaaao hahaha, como vimos antes, não podemos esquecer da aceleração de Coriolis.
Mas, a velocidade de em relação ao disco, pode ser dada por:
Logo:
Prontoo, agora sim podemos somar. Temos:
Logo, pra finalizar a questão:
Ufaa! Lá se foi mais uma questaozita.
Aproveita agora pra dar uma respirada, tomar uma água, e já volta na próxima questão 😊
Resposta
a)
b)
c)
d)