02) Um disco de massa e raio , articulado pelo seu centro a uma barra AO de massa e comprimento , rola sem escorregar sobre a superfície interna de uma pista fixa em forma de aro circular. O sistema parte do repouso quando a barra está alinhada com a direção horizontal (. A base de versores mostrada na figura é ligada à barra AO.
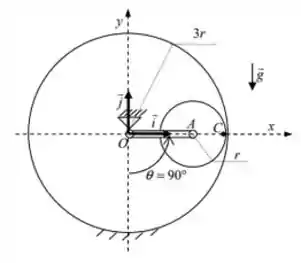
Para um ângulo arbitrário , pede-se:
a) Determinar a relação entre as velocidades angulares do disco e da barra e entre as acelerações angulares do disco e da barra ;
b) Desenhar os diagramas de corpo livre do disco e da barra;
c) Indicar as forças que realizam trabalho nulo, apresentando as devidas justificativas;
d) Escrever a expressão geral da energia cinética do sistema;
e) Determinar a velocidade angular do disco;
f) Determinar a aceleração angular do disco.
Passo 1
Ooii gente, tudo bom com vocês?
a) Pra começar precisamos determinar a relação tanto entre as velocidades angulares como entre as acelerações angulares do disco e da barra. O problema é que não tem uma equação que relacione direto essas grandezas. Então, como podemos fazer isso?

A ideia nesse tipo de questão é encontrarmos um ponto em comum à barra e ao disco para relacionar tais grandezas. Nessa questão, por exemplo, o ponto A relaciona-se com ambos, então vamos usá-lo.
Olhando para o disco, podemos escrever:
Como o disco rola sem escorregar, temos:
Olhando agora para a barra, como O é um ponto fixo, temos:
Igualando as duas expressões para a velocidade de A, vem:
Boa! Pra encontrar a relação entre as acelerações angulares basta a gente derivar em relação ao tempo dos dois lados da equação, daí:
Passo 2
b) Devemos desenhar o diagrama de corpo livre do disco e da barra, para uma inclinação genérica. Vamos identificar as forças que estão agindo neles.
Começando pelo disco, além da força peso, há também as reações da articulação em A, bem como as reações no contato do disco com o aro. Daí, podemos desenhar o seguinte diagrama:
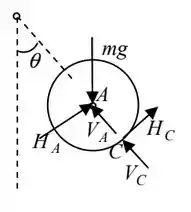
Indo agora para a barra, temos também as reações na articulação em A (que deverão estar em sentido oposto ao dessas reações no disco), as reações na articulação em O e a força peso atuando no meio da barra. Aí ficamos com:
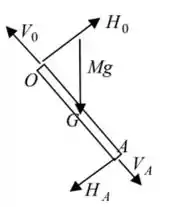
Passo 3
c) Agora precisamos identificar quais forças realizam trabalho nulo, ou seja, não fazem trabalho.
Primeiro, tomando a barra e disco como nosso sistema, forças internas a ele não realizam trabalho. É o caso, por exemplo, do par ação e reação atuando em A.
Anisando as forças externas, temos as reações em O. Mas como O é um ponto fixo, ele não apresenta deslocamento. Logo, o trabalho das forças e são nulos.
Temos também as reações em C, mas nesse ponto o disco rola sem escorregar, assim a velocidade do ponto C é sempre nula. Daí, o trabalho elementar realizado por essa força também é nulo.

Passo 4
d) Nesse item o enunciado nos pede para escrever a expressão geral para a energia cinética sistema (barra + disco), em um ângulo genérico. Essa angulação vai influenciar apenas no parâmetro da velocidade angular, então bora deixá-lo em função de . Daí, podemos escrever que:
Substituindo os valores do momento de inércia do disco e da barra, vem:
Usando nossa relação entre e , temos:
Prontinho 😊
Passo 5
e) Beleza galera, nesse item precisamos encontrar a velocidade angular do disco. A gente tem que ser esperto!

A questão muitas vezes vai direcionando a gente através dos itens, então mesmo se a gente não soubesse como encontrar a velocidade angular, seria uma ótima ideia aproveitar o resultado do item anterior e aplicar o teorema da energia cinética 😊

Aplicando esse teorema no nosso sistema entre o instante inicial ° com a vertical) e um instante qualquer, onde temos um ângulo genérico Lembrando que na situação inicial, o sistema parte do repouso, logo . Daí:
(Fica ligado que o segundo termo da equação é justamente o trabalho da força peso no disco e na barra). Daí:
Ufaa, agora só falta mais um item. Grandinha essa questão né pessoal? Mas bora lá, sem deixar a peteca cair Rs.
Passo 6
f) Beleza, pra encerrar precisamos determinar a aceleração angular do disco. Como já encontramos a velocidade angular, basta a gente derivar essa expressão. Pra facilitar a derivação, vamos derivar a seguinte expressão:
Logo:
Boaaaa! Conseguimos matar mais uma. É isso aí pessoal, espero que todo mundo tenha entendido. Espero vocês na próxima! Tamo junto 😉
Resposta
a)
b) Resolução no texto.
c) Resolução no texto.
d) Resolução no texto.
e)
f)