Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Relativo: Aceleração

Ver Teoria
Exercício 13123456789101112141516171819202122

Enunciado

USP, Mecânica, P2-2018.1, Questão 01

01) O mecanismo da figura ao lado é composto pelas barras AB e BC de mesmo comprimento a , articuladas entre si por meio de um pino B. A extremidade A da barra AB é vinculada a uma articulação fixa e a extremidade C da barra BC é ligada a um pistão que se move ao longo de uma guia vertical. Sabendo que, na configuração ilustrada, a barra AB gira com velocidade angular ω e aceleração angular ω ˙ , determine:

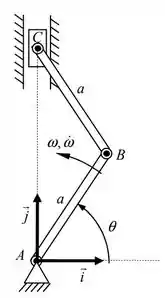
a) a velocidade e a aceleração do ponto B;

b) o centro instantâneo de rotação da barra BC;

c) a velocidade angular ω B C da barra BC e a velocidade do ponto C;

d) a aceleração angular ω ˙ B C da barra BC e a aceleração do ponto C.

Passo 1

Faaala galerinha do Responde Aí, tudo bem com vocês?

a) Bom, pra começar essa questão vamos determinar a velocidade e a aceleração do ponto B. É importante aqui lembrar das expressões para velocidade e aceleração em um movimento plano geral.

Temos que:

v → B = v → A + v → B / A  

Como A é um ponto fixo, vale que:

v → B = ω k → × B - A = ω k → × a c o s θ i → + a s e n θ j →

= ω a c o s θ j → - ω a s e n θ i →  

⇒ v → B = ω a ( - s e n θ ⋅ i → + c o s θ ⋅ j → )

Já para a aceleração, temos que:

a → B = a → A + ω ˙ k → × B - A - ω 2 ( B - A )

Como A é fixo, a → A = 0 . Logo:

a → B = ω ˙ k → × a c o s θ i → + a s e n θ j → - ω 2 a c o s θ i → + a s e n θ j →

∴ a → B = ω ˙ a c o s θ j → - ω ˙ a s e n θ i → - ω 2 a c o s θ i → + a s e n θ j →  

Portanto:

a → B = - ω 2 a c o s θ - ω ˙ a s e n θ i → + ω ˙ a c o s θ - ω 2 s e n θ j →  

Prontinho 😊

Passo 2

b) Aqui precisamos determinar o centro instantâneo de rotação (CIR) da barra BC.

Lembra que pra encontrar o CIR de uma barra, basta escolher dois pontos da barra de velocidades conhecidas e traçar uma reta perpendicular a direção de cada uma delas. O ponto de intersecção será o CIR.

Como no item anterior acabamos de determinar v → B , B será um dos nossos pontos. Lembrando que para esse ponto, sendo A um ponto fixo, logo CIR da barra AB, v → B é perpendicular a AB. Além disso, em C a velocidade é apenas vertical.

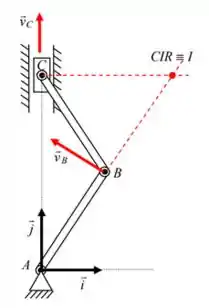
Massa! Encontramos o CIR de BC. Como B é ponto médio do lado BI do triângulo AIC, por semelhança de triângulos podemos afirmar que:

C I R B C = 2 a c o s θ i → + 2 a s e n θ j →

Foi!! 😊

Passo 3

c) Devemos determinar ω B C e v → C .

Gente, é bem importante aprendermos a surfar na onda da questão haha. A maioria desses exercícios de mecânica com várias letras, nos conduzem até a solução correta por meio desses itens. Então vê, no item anterior calculamos o CIR da barra BC. Bora usar esse cara pra resolver esse item.

Sabemos que:

v → B =   ω B C k → × r → B / I  

⇒ v → B =   ω B C k → × ( - a c o s θ i → - a s e n θ j → )

Logo:

ω a ( - s e n θ ⋅ i → + c o s θ ⋅ j → ) = ( - ω B C a c o s θ j → + ω B C a s e n θ i → )

∴   ω B C = ω

Muito bom! Agora precisamos calcular v → C . Ainda usando o CIR, temos:

v → C =   ω B C k → × r → C / I  

⇒ v → C =   - ω k → × - 2 a c o s θ i → = 2 ω a c o s θ j →

Ótimo! Matamos mais uma letra! Bora pra última 😊

Passo 4

d) Devemos determinar a aceleração angular ω ˙ B C e a aceleração a → C .

Sabemos que:

ω ˙ B C = d ω B C d t = d - ω d t =   - ω ˙

Boa! Usando a aceleração para um movimento plano geral, temos também que:

a → C =   a → B +   ω ˙ B C k → × r → C / B   - ω B C 2 r → C / B

Pelos itens anteriores, substituindo alguns resultados encontrados, temos que:

a → C = - ω 2 a c o s θ - ω ˙ a s e n θ i → + ω ˙ a c o s θ - ω 2 s e n θ j →   + ω ˙ B C k → × - a c o s θ i → +   a s e n θ j → - ω B C 2 - a c o s θ i → + a s e n θ j →

Logo:

a → C = - ω 2 a c o s θ - ω ˙ a s e n θ - ω ˙ B C a s e n θ + ω B C 2 a c o s θ i → + ω ˙ a c o s θ - ω 2 s e n θ - ω ˙ B C a c o s θ - ω B C 2 a s e n θ j →  

Fazendo ω B C =   - ω e ω ˙ B C =   - ω ˙ , ficamos com:

a → C = 0 i → + 2 a ω ˙ c o s θ - ω 2 s e n θ j →

Aeee, conseguimos finalizar a questão! Espero que todos vocês tenham entendido. Até a próxima pessoal 😊

Resposta

a)

v → B = ω a - s e n θ ⋅ i → + c o s θ ⋅ j →

a → B = - ω 2 a c o s θ - ω ˙ a s e n θ i → + ω ˙ a c o s θ - ω 2 s e n θ j →  

b) C I R B C = 2 a c o s θ i → + 2 a s e n θ j →

c)

ω B C = ω

v → C =   2 ω a c o s θ j →

d)

ω ˙ B C = - ω ˙

a → C = 0 i → + 2 a ω ˙ c o s θ - ω 2 s e n θ j →

Exercícios de Livros Relacionados

Se a extremidade A da barra restrita possui uma velocidade constante para eixo v A de 2 m/s quando a barra passa pela posição para qual θ = 30 ° , determine a aceleração do centro de massa G no meio d
15.222. A placa circular mostrada na figura gira em torno de seu diâmetro vertical a uma taxa constante 1 10 rad /s. Sabendo que na posição mostrada o disco se encontra no plano XY e o ponto D da alça
O mecanismo de dois membros serve para amplificar o movimento angular. O membro AB tem um pino em B que está confinado a se deslocar dentro da ranhura do membro CD. Se, no instante mostrado, AB (entra
A argola é lançada na superfície áspera de maneira que ela tem uma velocidade angular ω = 4r a d / s e uma aceleração angular α = 5r a d / s 2 . Além disso, seu centro tem uma velocidade v O = 5m / s
O cilindro hidráulico D se estende com a velocidade v B = 1,2m / s e uma aceleração a B = 0,45m / s 2 . Determine a aceleração de A no instante mostrado.