Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Relativo: Aceleração

Ver Teoria
Exercício 51234678910111213141516171819202122

Enunciado

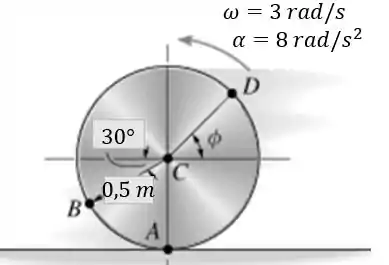
O disco está se deslocando para a esquerda com aceleração angular α = 8   r a d / s 2 e a velocidade angular ω = 3   r a d / s . Se ele não escorrega em A , determine a aceleração do ponto B .

Passo 1

Nosso primeiro passo é relacionar o ponto que queremos saber as informações (ponto B ) com um ponto que já temos algum dado ou que pelo menos conseguimos saber as informações dele de um jeito fácil.

O centro do disco O vai ser o nosso ponto, pois sua aceleração será:

a O = α r     →       a O = 8 ( 0,5 )

a O = 4   m / s 2

E quanto ao seu sentido? Como o disco não sofre uma desaceleração (a aceleração angular está no mesmo sentido da velocidade angular), então a aceleração do ponto O está no sentido do movimento:

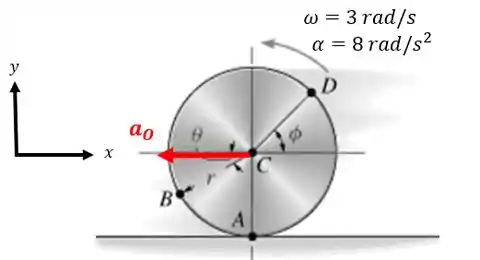
Então:

a → O = - 4 i ^   m / s 2

Feito isso, vamos montar nossa equação da aceleração:

a → B = a → O + α × r → B / O - ω 2 r → B / O

Vamos ter o seguintes vetor r → B / O :

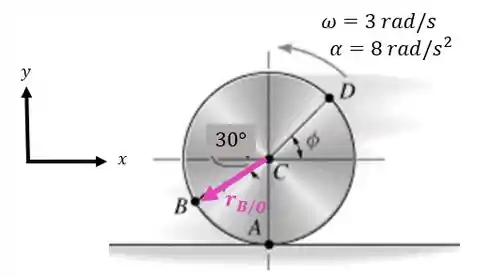
Vamos decompor os vetores para fazermos o produto vetorial. O vetor r → B / O pode ser escrito como:

r → B / O = ( - 0,5 cos ⁡ 30 ° i ^ - 0,5 s e n   30 °   j ^ )

r → B / O = - 0,433 i ^ - 0,25 j ^   m

Repare que a aceleração do ponto B é a resultante entre a aceleração tangencial e a normal:

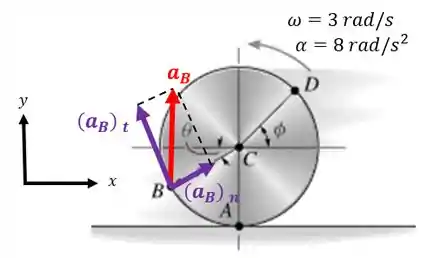
Então, podemos escrever o vetor aceleração do ponto B em função de suas componentes x e y :

a → B = a B i ^ + a B j ^

A aceleração angular e a velocidade angular fazem o disco girar no sentido anti-horário, ou seja, as duas são positivas de acordo com a nossa convenção de sinais:

ω → = 3 k ^   r a d / s

α → = 8 k ^   r a d / s 2

Passo 2

Vamos substituir o que temos até agora na nossa equação:

a → B = a → O + α × r → B / O - ω 2 r → B / O

∴

a B i ^ + a B j ^ = - 4 i ^ + ( 8 k ^ ) × - 0,433 i ^ - 0,25 j ^ - ( 3 ) 2 - 0,433 i ^ - 0,25 j ^

Vamos ter que:

a B i ^ + a B j ^ = - 4 i ^ + ( 8 k ^ ) × - 0,433 i ^ - 0,25 j ^ - 9 - 0,433 i ^ - 0,25 j ^

∴

a B i ^ + a B j ^ = - 4 i ^ + ( 8 k ^ ) × - 0,433 i ^ - 0,25 j ^ + 3,897 i ^ + 2,25 j ^

Vamos fazer o produto vetorial separado:

α × r → B / O = ( 8 k ^ ) × - 0,433 i ^ - 0,25 j ^

i ^ j ^ k ^ 0 0 8 - 0,433 - 0,25 8 0 = i ^ 0 8 - 0,25 0 - j ^ 0 8 - 0,433 0 + k ^ 0 0 - 0,433 - 0,25

α × r → B / O = 2 i ^ - 3,464 j ^

Agora é só substituir:

a B i ^ + a B j ^ = - 4 i ^ + ( 8 k ^ ) × - 0,433 i ^ - 0,25 j ^ + 3,897 i ^ + 2,25 j ^

∴

a B i ^ + a B j ^ = - 4 i ^ + 2 i ^ - 3,464 j ^ + 3,897 i ^ + 2,25 j ^

Vamos separar as equações de acordo com as componentes x e y :

E m   x     →       a B = - 4 + 2 + 3,897

E m   y     →       a B = - 3,464 + 2,25

Então, a componente x da aceleração do ponto B será:

a → B x = 1,90 i ^

E a componente y será:

a → B y = - 1,21 j ^

A resultante será:

a B = ( a B x ) 2 + ( a B y ) 2     →         a B = ( 1,90 ) 2 + ( - 1,21 ) 2

a B = 2,25   m / s 2

Resposta

a )   a B = 2,25   m / s 2

Exercícios de Livros Relacionados

Se a extremidade A da barra restrita possui uma velocidade constante para eixo v A de 2 m/s quando a barra passa pela posição para qual θ = 30 ° , determine a aceleração do centro de massa G no meio d
15.222. A placa circular mostrada na figura gira em torno de seu diâmetro vertical a uma taxa constante 1 10 rad /s. Sabendo que na posição mostrada o disco se encontra no plano XY e o ponto D da alça
O mecanismo de dois membros serve para amplificar o movimento angular. O membro AB tem um pino em B que está confinado a se deslocar dentro da ranhura do membro CD. Se, no instante mostrado, AB (entra
A argola é lançada na superfície áspera de maneira que ela tem uma velocidade angular ω = 4r a d / s e uma aceleração angular α = 5r a d / s 2 . Além disso, seu centro tem uma velocidade v O = 5m / s
O cilindro hidráulico D se estende com a velocidade v B = 1,2m / s e uma aceleração a B = 0,45m / s 2 . Determine a aceleração de A no instante mostrado.