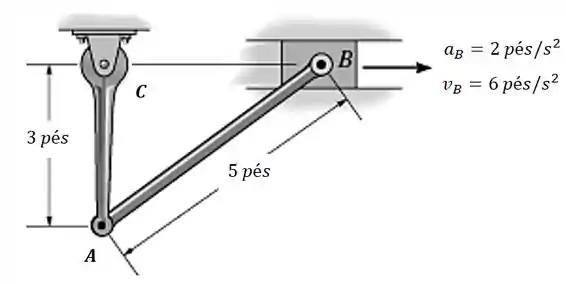
O bloco deslizante move-se para a direita com aceleração de . Na situação mostrada na figura, a velocidade de é de . Determine a aceleração angular da barra e a aceleração do ponto , na situação considerada.
Passo 1
Vamos começar resolvendo esta questão relacionando os pontos e , pois temos alguma informação sobre o movimento do ponto . Podemos relacionar a velocidade destes pontos usando a seguinte equação:
A velocidade do ponto foi dada e vale:
A velocidade angular da barra nós não sabemos, mas vamos arbitrar como positiva:
E o vetor posição relativa é:
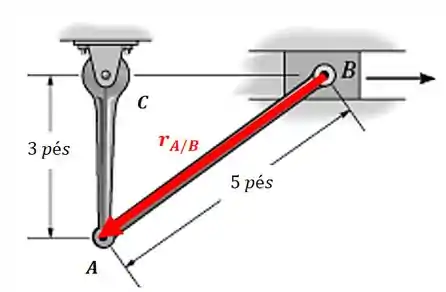
Vamos ter o seguinte triângulo retângulo:
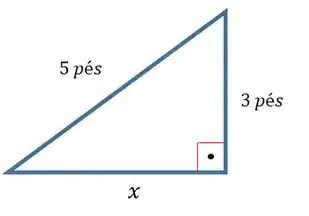
Usando o Teorema de Pitágoras conseguimos achar o valor de :
Então, o vetor posição será:
Agora que já identificamos cada termo da equação é só substituirmos:
Esse produto vetorial fica:
Substituindo isso na nossa equação:
Mas somente com esta equação não conseguimos determinar o valor da velocidade do ponto , temos que arranjar outro jeito de achar a velocidade deste ponto.
Passo 2
Outra forma de achar a velocidade do ponto é usarmos a barra :
Repare que o ponto gira em torno do ponto que está fixo. Dessa maneira, a velocidade do ponto é zero:
Nós não sabemos o valor da velocidade angular da barra , mas vamos arbitrar seu sentido como positivo:
E o vetor posição será:
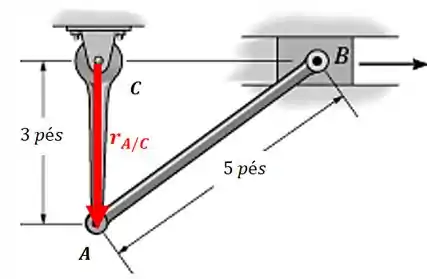
Substituindo na nossa equação:
Resolvendo esse produto vetorial obtemos:
Agora vamos resgatar a outra equação para determinar a velocidade do ponto :
Igualando as duas, temos que:
Agora vamos separar as equações de acordo com as componentes e :
Da segunda equação tiramos que:
E da primeira equação temos que:
Como o valor deu positivo, significa que arbitramos o sentido correto:
Passo 3
Agora vamos relacionar as acelerações dos pontos e :
Já sabemos que:
E que:
Não sabemos o valor da aceleração angular da barra , mas vamos arbitrar como positiva:
Substituindo tudo isso na nossa equação, temos que:
Resolvendo o produto vetorial, temos que:
Então, nossa equação fica:
Vamos guardar esta informação, porque só com ela não conseguimos avançar na questão.
Passo 4
Vamos usar a barra para termos outra equação para a aceleração do ponto . Como o ponto gira em torno de um ponto fixo, podemos escrever:
Já sabemos desta equação que:
E:
Nós não sabemos a aceleração angular, mas vamos arbitrá-la como positiva:
Substituindo tudo isso, temos que:
Resolvendo o produto vetorial:
Então, nossa equação fica:
Passo 5
Nosso próximo passo é igualar as duas equações para aceleração do ponto que temos:
E:
Então, vamos ter que:
Vamos separar as equações de acordo com as componentes e :
Da segunda equação obtemos que:
Como achamos um valor negativo, significa que arbitramos o sentido contrário para a aceleração angular da barra :
Essa é a nossa primeira resposta. Falta acharmos a aceleração do ponto .
Para isso, vamos resgatar a equação que já montamos anteriormente:
Temos que:
Esse produto vetorial fica:
Então:
E o seu módulo fica:
Vamos achar também o ângulo de inclinação deste vetor. Para isso, vamos desenhá-lo:
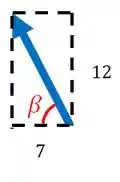
Temos que:
Então: