01) A plataforma circular de raio gira em torno do eixo vertical fixo com velocidade angular (constante) e desliza na direção do mesmo eixo com velocidade , conforme mostrado na figura. Uma barra de comprimento é articulada na plataforma em , e gira com velocidade angular (constante) em relação à plataforma. Para a configuração instantânea indicada, e admitindo a plataforma como referencial móvel, calcule e escreve suas respostas nos campos abaixo utilizando o sistema de coordenadas solidário à plataforma.
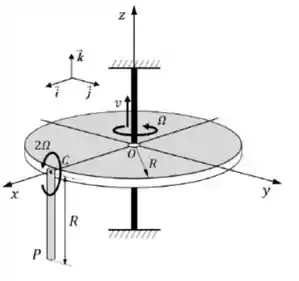
a) As velocidades relativa, de arrastamento e absoluta do ponto da barra.
b) As acelerações relativa, de arrastamento e absoluta do ponto da barra.
c) O vetor rotação absoluta da barra.
d) O vetor aceleração rotacional absoluta da barra.
Passo 1
Faaala gente bonita do Responde Aí, como vocês estão?
Aqui temos uma plataforma girando e deslizando em torno do eixo , e uma barra presa na plataforma, girando em torno do eixo .
a) Nesse item devemos determinar as velocidades relativa em relação a plataforma, de arrastamento e absoluta do ponto , que se localiza na extremidade da barra.
A gente sabe que nas equações de mecânica, pra escrever a velocidade de um ponto costumamos pegar outro como referência, certo? Qual o ponto que a gente deve usar para calcular a velocidade de em relação a plataforma?

É justamente o ponto . Ele é muito bom porque pertence tanto à barra CP como à plataforma, sacaram?! Então bora lá:
Nota que, como pertence a plataforma e está fixo nela, sua velocidade relativa é nula. Assim, vem:
Top! Vamos agora para a de arrastamento, que basicamente é a componente do movimento de que é feita pela plataforma. Por isso, como a plataforma gira em relação a origem, é uma boa fazermos tudo em relação a ela:
Como a plataforma está deslizando no eixo com velocidade , em relação a temos:
Perfeito!
Para matar esse item, basta descobrir a velocidade absoluta, que é simplesmente a soma das velocidades:
Essa já foi!! 😊
Passo 2
b) Aqui precisamos determinar praticamente as mesmas coisas do item anterior, mas no lugar de ser a velocidade, é a aceleração.
A ideia é usar equação da aceleração no movimento plano geral, lembram:
Essa é a forma geral, mas vamos começar com a . Novamente, escolhendo o ponto , temos:
Como as acelerações e , pois a velocidade de rotação da barra em torno do eixo é constante, temos:
Show! Indo agora para o cálculo da aceleração de arrastamento, vamos novamente usar o ponto como referência:
Como a plataforma desliza e gira com velocidade constante, podemos reescrever a equação:
Logo:
Muito bom!
Pra finalizar precisamos calcular a aceleração absoluta, mas aqui temos que ter um certo cuidado. Nesse tipo de movimento, em que o ponto rotaciona em torno de um ponto que já está rotacionando e transladando (o ponto ), surge também a aceleração de Coriolis. Assim:
Prontoo! Agora sim podemos calcular a aceleração absoluta. Ela será dada por:
Portanto:
Prontinho 😊
Passo 3
c) Aqui precisamos calcular o vetor rotação absoluta da barra .
Mas, ele é simplesmente como a velocidade angular resultante dos dois tipos de movimento realizado pela barra: o de arrastamento e o relativo ao eixo . Daí:
Massa! Esse foi rápido.
Passo 4
d) Chegamos no último item, ufa!!!
Pra encerrar, devemos calcular o vetor aceleração rotacional da barra. É basicamente uma aceleração angular resultante, mas com um termo a mais. É dada pela expressão:
Como já vimos nos itens anteriores:
Assim:
Logo, pra finalizar:
Aeee, matamos mais uma questão.Espero que vocês tenham entendido bem direitinho, até a próxima galera 😉
Resposta
a) Resolução no texto.
b) Resolução no texto.
c)
d)