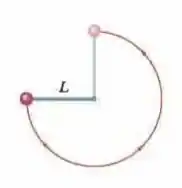
(Capítulo 8.4 – Exercício 2) A Fig. 8-29 mostra uma bola de massa presa à extremidade de uma haste fina de comprimento e massa desprezível. A outra extremidade da haste é articulada, de modo que a bola pode se mover em uma circunfêrencia vertical. A haste é mantida na posição horizontal, como na figura, e depois recebe um impulso para baixo com força suficiente para que a bola passe pelo ponto mais baixo da circunferência e continue em movimento até chegar ao ponto mais alto com velocidade nula. Qual é o trabalho realizado sobre a bola pela força gravitacional do ponto inicial até (a) o ponto mais baixo, (b) o ponto mais alto, (c) o ponto à direita na mesma altura que o ponto inicial? Se a energia potencial gravitacional do sistema bola-Terra é tomada como zero no ponto inicial, determine o seu valor quando a bola atinge (d) o ponto mais baixo, (e) o ponto mais alto e (f) o ponto à direita na mesma altura que o ponto inicial. (g) Suponha que a haste tenha recebido um impulso maior e passe pelo ponto mais alto com uma velocidade diferente de zero. A variação do ponto mais baixo ao ponto mais alto é maior, menor ou a mesma que quando a bola chegava ao ponto mais alto com velocidade zero?
Passo 1
E aííí gente, tudo belezinha?
Se liga, a gente sabe que a força peso é uma força conservativa, então podemos calcular o trabalho realizado por esta força usando o seguinte teorema:
Assim, reescrevendo com a equação da energia potencial:
Podemos perceber que o peso só realiza trabalho se ocorrer variação da altura. Para esta questão, vamos considerar que o nosso coincide com o ponto mais baixo alcançado pela bolinha, ok?
Vamos lá!
Passo 2
a) Analisando o ponto de partida e o ponto mais baixo, a variação de altura é:
Assim:
Substituindo os valores:
Passo 3
b) Do ponto de partida até o ponto mais alto, a variação de altura é:
Assim:
Passo 4
c) Do ponto de partida até o ponto mais a direita, a variação de altura é:
Assim:
Passo 5
d) Agora, nosso ponto de não é mais o ponto mais baixo, é o ponto de partida. Essa consideração vai ser empregada para todas as etapas posteriores.
Analisando o ponto de partida e o ponto mais baixo, a variação de altura é:
Assim:
Passo 6
e) Analisando o ponto de partida e o ponto mais alto, a variação de altura é:
Assim:
Passo 7
f) Analisando o ponto de partida e o ponto mais a direita, a variação de altura é:
Assim:
Passo 8
g) Ao escrevermos a equação para , percebemos que ela só depende da variação da altura, portanto, o módulo da velocidade com que ela passará nos pontos não interfere no cálculo. O resultado será igual.
Fechouuu?
Resposta
- ;
- ;
- ;
- ;
- ;
- ;
- .