Um corpo de massa é suspenso por um fio ideal, mantido esticado, de comprimento , que está preso ao teto. Se o corpo é abandonado a partir de um ponto em que o fio faz um ângulo com a vertical, os trabalhos realizados pelo peso do corpo, , e pela tensão no fio, , entre o ponto inicial e o ponto em que se encontra na posição vertical valem, respectivamente:
Passo 1
Começando pelo mais tranquilo, vamos analisar o trabalho da força tração
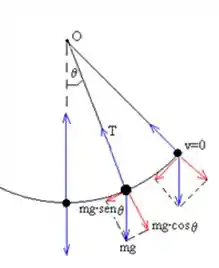
Se lembra da formula do trabalho?
Então, como aqui a força é sempre perpendicular a trajetória, o trabalho vai ser . A força tração ocupa a mesma posição do raio em uma curva, por o ângulo é .
Passo 2
Já a força peso nós sabemos pela fórmula que o trabalho da força peso é:
Mas esse a gente pode descobrir usando uma geometria no problema.
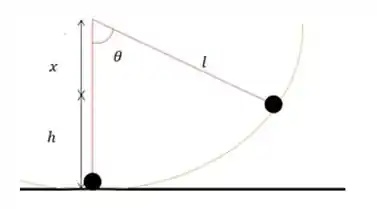
O que interessa pra gente é aquele ali, sendo que ele vai ser o comprimento inteiro do fio menos aquele , que é o do triângulo inicial
Sendo assim:
Resposta
Letra A