UFRJ – Física 1 – P2 – 2019.2 – Questão 7
Uma partícula de massa move-se sobre uma calha horizontal lisa. A calha horizontal transforma-se,
suavemente, a partir do ponto , em uma calha semicircular de raio , tal como indicado na figura.
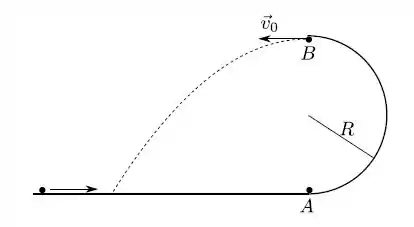
A partícula deixa a calha semicircular no ponto , que se encontra exatamente acima do ponto , com velocidade horizontal . Em relação ao trabalho realizado pela força gravitacional que atua sobre a partícula no trajeto entre os pontos A e B, é CORRETO afirmar que
(a)
(b)
(c)
(d)
(e)
Passo 1
Se liga! Aqui precisamos lembrar que o trabalho pode ser escrito como
Levando em consideração que estamos tratando da força peso, temos que
Passo 2
Podemos considerar que a força peso é uma força conservativa. Sendo assim, o trabalho não dependerá do caminho. Apenas da distância entre o ponto inicial e o ponto final.
No caso do nosso exercício, a distância entre os pontos e
Passo 3
Agora se liga, como a partícula está se deslocando para cima e a força peso puxa para baixo, temos que o ângulo entre essas direções é 180°. Portanto
Substituindo os valores na expressão do trabalho, teremos que
A alternativa correta é a letra (a).